题目内容
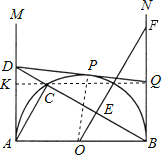
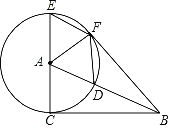
【题目】如图,![]() 是半圆
是半圆![]() 的直径,
的直径,![]() .射线
.射线![]() 为半圆
为半圆![]() 的切线.在
的切线.在![]() 上取一点
上取一点![]() ,连接
,连接![]() 交半圆于点
交半圆于点![]() ,连接
,连接![]() .过
.过![]() 点作
点作![]() 的垂线
的垂线![]() ,垂足为点
,垂足为点![]() ,与
,与![]() 相交于点
相交于点![]() .过
.过![]() 点作半圆
点作半圆![]() 的切线
的切线![]() ,切点为
,切点为![]() ,与
,与![]() 相交于点
相交于点![]() .
.

(1)求证:![]() ∽
∽![]() ;
;
(2)当![]() 与
与![]() 的面积相等时,求
的面积相等时,求![]() 的长;
的长;
(3)求证:当![]() 在
在![]() 上移动时(
上移动时(![]() 点除外),点
点除外),点![]() 始终是线段
始终是线段![]() 的中点.
的中点.
【答案】(1)证明见解析;(2)BQ=1;(3)证明见解析.
【解析】
(1)根据OE∥AC,得出∠BAC=∠FOB,进而得出∠BCA=∠FBO=90°,从而证明结论;
(2)根据△ACB∽△OBF得出△ABD∽△BFO,从而得出DQ∥AB,即可得出BQ=AD;
(3)首先得出AD=DP,QB=BQ,进而得出DQ2=QK2+DK2,得出BF=2BQ,即可得出Q为BF的中点.
解:(1)证明:∵AB为直径,
∴∠ACB=90°,即:AC⊥BC,
又OE⊥BC,
∴OE∥AC,
∴∠BAC=∠FOB,
∵BN是半圆的切线,
∴∠BCA=∠FBO=90°,
∴△ABC∽△OFB.
(2)连接OP,
由△ACB∽△OBF得,∠OFB=∠DBA,∠BCA=∠FBO=90°,
∵AM、BN是⊙O的切线,
∴∠DAB=∠OBF=90°,
∴△ABD∽△BFO,
∴当△ABD与△BFO的面积相等时,△ABD≌△BFO,
∴AD=OB=1,
∵DP切圆O,DA切圆O,
∴DP=DA,
∵△ABD≌△BFO,
∴DA=BO=PO=DP,
又∵∠DAO=∠DPO=90°,
∴四边形AOPD是正方形,
∴DQ∥AB,
∴四边形ABQD是矩形,
∴BQ=AD=1;
(3)证明:由(2)知,△ABD∽△BFO,
∴![]() =
=![]() ,
,
∴BF=![]() =
=![]() =
=![]() ,
,
∵DP是半圆O的切线,射线AM、BN为半圆O的切线,
∴AD=DP,QB=QP,
过Q点作AM的垂线QK,垂足为K,在Rt△DQK中,
DQ2=QK2+DK2,
∴(AD+BQ)2=(AD﹣BQ)2+22.
∴BQ=![]() ,
,
∴BF=2BQ,
∴Q为BF的中点.