Question

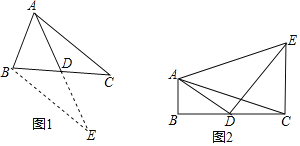
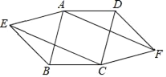
【题目】如图，四边形ABCD是平行四边形，分别以AB，CD为边向外作等边△ABE和△CDF，连接AF，CE．求证：四边形AECF为平行四边形．

Answer 1

【答案】见解析.

【解析】

由平行四边形的性质可得AB＝CD，AD＝BC，∠ABC＝∠ADC，由等边三角形的性质可得BE＝EA＝AB＝CD＝CF＝DF，∠EBA＝∠CDF＝60°，由“SAS”可证△ADF≌△CBE，可得EC＝AF，由两组对边相等的四边形是平行四边形可证四边形AECF为平行四边形．

∵四边形ABCD是平行四边形

∴AB＝CD，AD＝BC，∠ABC＝∠ADC

∵△ABE和△CDF是等边三角形

∴BE＝EA＝AB＝CD＝CF＝DF，∠EBA＝∠CDF＝60°

∴∠ADF＝∠EBC，且AD＝BC，BE＝DF

∴△ADF≌△CBE（SAS）

∴EC＝AF，且AE＝CF

∴四边形AECF为平行四边形.