题目内容
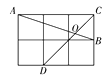
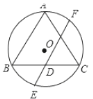
【题目】已知如图，△ABC是⊙O的内接正三角形，弦EF经过BC边的中点D，且EF∥BA，若⊙O的半径为
， 则DE的长为（ ）
A. 
B. 
C. 
D. 
【答案】C
【解析】
根据等边三角形的性质求得圆的半径，然后根据中位线定理求得DG的长，利用勾股定理求得EG，即可求得EF的长，根据ED=
即可求解
连接OC交EF于M，延长CM交AB于点H．连接OA，连接OE．
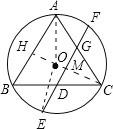
在直角△OAH中，AH＝OAcos30°＝
＝2
∴AB＝2AH＝4
又∵弦EF经过BC边的中点D，且EF∥BA．
∴DG＝
AB＝2，
在直角△ACH中，CH＝ACsin60°＝4×
＝2
，
∴OH＝
CH＝
，
HM＝CH＝，
∴OM＝HM﹣OH＝
，
在直角△OME中，EM＝
＝
，
∴EF＝2，
∴ED＝＝﹣1．
故选：C．
练习册系列答案
相关题目
【题目】某批发商以每件50元的价格购进400件T恤．若以单价70元销售,预计可售出200件．批发商的销售策略是：第一个月为增加销售量,降价销售,经过市场调查,单价每降低0.5元,可多售出5件,但最低单价不低于购进的价格;第一个月结束后,将剩余的T恤一次性清仓销售,清仓时单价为40元．设第一个月单价降低x元．
（1）根据题意,完成下表：
每件T恤的利润（元） | 销售量（件） | |
第一个月 | ||
清仓时 |
（2）T恤的销售单价定为多少元时,该批发商可获得最大利润？最大利润为多少？
