Question

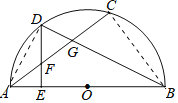
【题目】如图，AB是半圆的直径，AC是一条弦，D是AC的中点，DE⊥AB于点E且DE交AC于点F，DB交AC于点G，若，则=_____．

Answer 1

【答案】

【解析】由AB是直径，推出∠ADG=∠GCB=90°，因为∠AGD=∠CGB，推出cos∠CGB=cos∠AGD，可得，设EF=3k，AE=4k，则AF=DF=FG=5k，DE=8k，想办法求出DG、AG即可解决问题；

连接AD，BC．

∵AB是半圆的直径，

∴∠ADB=90°，又DE⊥AB，

∴∠ADE=∠ABD，

∵D是的中点，

∴∠DAC=∠ABD，

∴∠ADE=∠DAC，

∴FA=FD；

∵∠ADE=∠DBC，∠ADE+∠EDB=90°，∠DBC+∠CGB=90°，

∴∠EDB=∠CGB，又∠DGF=∠CGB，

∴∠EDB=∠DGF，

∴FA=FG，

∵，设EF=3k，AE=4k，则AF=DF=FG=5k，DE=8k，

在Rt△ADE中，AD=，

∵AB是直径，

∴∠ADG=∠GCB=90°，

∵∠AGD=∠CGB，

∴cos∠CGB=cos∠AGD，

∴，

在Rt△ADG中，DG=k，

∴，

故答案为：．