题目内容
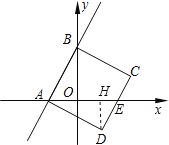
【题目】如图，一次函数y＝2x+4的图象与x、y轴分别相交于点A、B，四边形ABCD是正方形．
（1）求点A、B、D的坐标；
（2）求直线BD的表达式．
【答案】（1）A（﹣2，0），点B（0，4），D（2，﹣2）；（2）y＝﹣3x+4．
【解析】
(1)由于ー次函数y=2x+4的图象与x、y轴分别相交于点A、B,所以利用函数解析式即可求出AB两点的坐标,然后过D作DH⊥x轴于H点,由四边形ABCD是正方形可以得到∠BAD=∠AOB=∠AHD=90°,AB=AD,接着证明△ABO≌△DAH,最后利用全等三角形的性质可以得到DH=AO=2,AH=BO=4,从而求出点D的坐标;
（2）利用待定系数法即可求解
解：（1）∵当y＝0时，2x+4＝0，x＝﹣2．
∴点A（﹣2，0）．
∵当x＝0时，y＝4．
∴点B（0，4）．
过D作DH⊥x轴于H点，
∵四边形ABCD是正方形，
∴∠BAD＝∠AOB＝∠AHD＝90°，AB＝AD．
∴∠BAO+∠ABO＝∠BAO+∠DAH，
∴∠ABO＝∠DAH．
∴△ABO≌△DAH．
∴DH＝AO＝2，AH＝BO＝4，
∴OH＝AH﹣AO＝2．
∴点D（2，﹣2）．
（2）设直线BD的表达式为y＝kx+b．
∴
解得
，
∴直线BD的表达式为y＝﹣3x+4．
练习册系列答案
相关题目
【题目】为了保护环境，某集团决定购买
、
两种型号的污水处理设备共10台，其中每台价格及月处理污水量如下表：
|
| |
价格（万元/元） | 15 | 12 |
处理污水量（吨/月） | 250 | 220 |
经预算，该集团准备购买设备的资金不高于130万元.
（1）请你设计该企业有哪几种购买方案？
（2）试通过计算，说明哪种方案处理污水多？
