Question

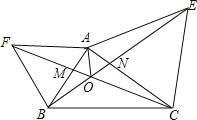
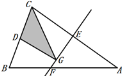
【题目】如图，等腰三角形ABC的底边BC长为4，面积是18，腰AC的垂直平分线EF分别交AC，AB边于E，F点．若点D为BC边的中点，点G为线段EF上一动点，则△CDG周长的最小值为（ ）

A.7B.9C.11D.13

Answer 1

【答案】C

【解析】

连接AD，由于△ABC是等腰三角形，点D是BC边的中点，故AD⊥BC，再根据三角形的面积公式求出AD的长，再再根据EF是线段AC的垂直平分线可知，点C关于直线EF的对称点为点A，故AD的长为CG+GD的最小值，由此即可得出结论．

解：连接AD，

∵△ABC是等腰三角形，点D是BC边的中点，
∴AD⊥BC，
∴S△ABC= BCAD= ×4×AD=18，解得AD=9，
∵EF是线段AC的垂直平分线，
∴点C关于直线EF的对称点为点A，
∴AD的长为CG+GD的最小值，
∴△CDG的周长最短=（CG+GD）+CD=AD+BC=9+ ×4=9+2=11．

故选C.