题目内容
【题目】如图1,直角坐标系中,点![]() 分别在
分别在![]() 轴上,点
轴上,点![]() 的坐标为
的坐标为![]() .以
.以![]() 为边在第一象限作等边
为边在第一象限作等边![]() 垂直平分
垂直平分![]() .
.
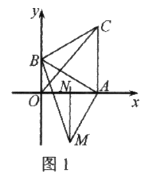
(1)求![]() 的长.
的长.
(2)求证:![]() .
.
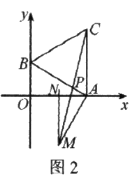
(3)如图2,连接![]() 交
交![]() 于点
于点![]() .点
.点![]() 是否为MC的中点?请说明理由.
是否为MC的中点?请说明理由.
【答案】(1)4;(2)见解析;(3)点![]() 为
为![]() 的中点,见解析
的中点,见解析
【解析】
(1)先利用直角三角形中,30°角所对的直角边等于斜边的一半直接求出AB;(2)因为根据条件可得∠OAC =∠MAB =90°,再证![]() ,由
,由![]() 是等边三角形,得出
是等边三角形,得出![]() ,从而证明
,从而证明![]() ,即可解答;(3)作
,即可解答;(3)作![]() 于
于![]() ,根据条件可得:
,根据条件可得:![]() ,所以
,所以![]() ,由(2)AM=AO可得
,由(2)AM=AO可得![]() ,又因为以点P为顶点的对顶角相等,证明出
,又因为以点P为顶点的对顶角相等,证明出![]() ,从而求解.
,从而求解.
(1)解:![]() .
.
在![]() 中,
中,![]() .
.
(2)证明:如图1,![]() .
.
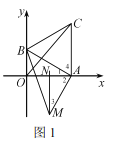
![]() 垂直平分
垂直平分![]() .
.
![]() .
.
![]() 是等边三角形,
是等边三角形,![]() .
.
![]() .
.
![]() .
.
![]()
(3)解:![]() 是
是![]() 的中点.理由如下:
的中点.理由如下:
如图2,作![]() 于
于![]() .
.

由己知,![]() .
.
![]() .
.
![]() .
.
由(2)AM=AO, 可得![]() .
.
![]() ,
,
![]() .
.
![]() .
.
即点![]() 为
为![]() 的中点.
的中点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目