题目内容
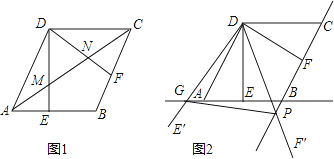
【题目】如图，AC是平行四边形ABCD的对角线，E、H分别为边BA和边BC延长线上的点，连接EH交AD、CD于点F、G，且EH∥AC．
（1）求证：EG=FH；
（2）若△ACD是等腰直角三角形，∠ACD=90°，F是AD的中点，AD=6，连接BF，求BF的长．
【答案】（1）见解析；（2）3
【解析】
（1）只要证明四边形ACHF是平行四边形，四边形ACGE是平行四边形，可得AC=HF=EG，即可推出EF=GH．
（2）首先证明∠BCF=90°．在Rt△BCF中，利用勾股定理即可解决问题；
（1）∵四边形ABCD是平行四边形，∴AD∥BC，AB∥CD．
∵AC∥EH，∴四边形ACHF是平行四边形，四边形ACGE是平行四边形，∴AC=HF，AC=EG，∴FH=EG，∴EG=FH．
（2）连接CF．
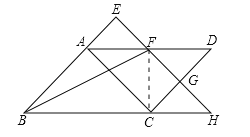
∵CA=CD，∠ACD=90°，AF=DF，∴CF⊥AD，CF=
AD．
∵AD∥BC，∴CF⊥BC，∴∠BCF=90°，
∵BC=AD=6，CF=AD=3，∴BF=
=3．
练习册系列答案
相关题目
