��Ŀ����
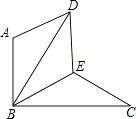
����Ŀ����ͼ��ƽ���ı��� ABCD ����AD��BC��AB=BC=CD=AD=4����A=��C=60�������� BD������BCD �Ƶ� B ��ת���� BD���� BD�䣩�� AD ����һ�� E��BC���� BC����ͬʱ�� CD ����һ�� F ʱ�����н�����ȷ���ǣ� ��
��AE=DF���ڡ�BEF=60�㣻�ۡ�DEB=��DFB���ܡ�DEF ���ܳ�����Сֵ��4+2![]()
A. �٢� B. �ڢ� C. �٢ڢ� D. �٢ڢۢ�
���𰸡�C
��������
���������֤��ABE�ա�BDF�����жϢ٢ڢ����ɡ�DEF���ܳ�=DE+DF+EF=AD+EF=4+EF����EF��Сʱ��DEF���ܳ���С�����ݴ��߶�������ɵ�BE��ADʱ��BE��С����EF��С���������ʱ��BDE�ܳ���Сֵ��
��AB=BC=CD=AD=4����A=��C=60�㣬
���ABD����BCDΪ�ȱ������������A=��BDC=60�㣮
�߽���BCD�Ƶ�B��ת����BC'D'λ����
���ABD'=��DBC'����AB=BD����A=��DBC'��
���ABE�ա�BFD��
��AE=DF��BE=BF����AEB=��BFD��
���BED+��BFD=180�㣮
�ʢ���ȷ���۴�����
�ߡ�ABD=60�㣬��ABE=��DBF��
���EBF=60�㣮
�ʢ���ȷ��
�ߡ�DEF���ܳ�=DE+DF+EF=AD+EF=4+EF��
�൱EF��Сʱ���ߡ�DEF���ܳ���С��
�ߡ�EBF=60�㣬BE=BF�����BEF�ǵȱ���������
��EF=BE��
�൱BE��ADʱ��BE������С����EF������С��
��AB=4����A=60�㣬BE��AD��
��EB=2![]() ��
��
���DEF���ܳ���СֵΪ4+2![]() ��
��
�ʢ���ȷ��
��ѡC��

 ��У��������ĩ��̾�ϵ�д�
��У��������ĩ��̾�ϵ�д�