题目内容
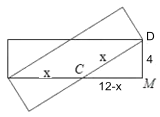
【题目】如图，两张完全相同的长方形纸片（长为12，宽为4）如图叠放在一起，重叠部分为四边形ABCD，则四边形ABCD的周长最大值为____．
【答案】
【解析】
首先可判断重叠部分为平行四边形，且两条纸条宽度相同；再由平行四边形的面积可得邻边相等，则重叠部分为菱形；设菱形的边长为x，根据勾股定理求出周长即可．
解答：解：由题意得：AB∥CD，AD∥BC，
∴四边形ABCD是平行四边形，
∵用两张等宽的纸条交叉叠放在一起，重叠部分为四边形ABCD，
SABCD＝BC×宽＝CD×宽，
∴BC＝CD，
∴四边形ABCD是菱形．
当两张纸条如图所示放置时，菱形周长最大，
设这时菱形的边长为xcm，
在Rt△MBD中，
由勾股定理：x2＝（12x）2＋42，
解得：x＝
，
∴4x＝，
即菱形的最大周长为cm．
故答案为：
练习册系列答案
相关题目
【题目】小明根据学习函数的经验，对函数
的图像与性质进行了探究．请补充完整：
（1）先填表，再在如图所示的平面直角坐标系中，描全表中各对对应值为坐标的点，并画出该函数的图像：
x | … | -5 | -4 | -3 | -2 | 0 | 1 | 2 | 3 | … |
| … | 2 |
| 3 | -3 |
| 0 | … |
（2）结合函数的图像，说出两条不同类型的性质；
①________________________________；____________________________________．
②的图像是由
的图像如何平移得到？
___________________________________________．
（3）当函数值
时，x的取值范围是____________span>．
