题目内容
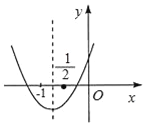
【题目】小明根据学习函数的经验,对函数![]() 的图像与性质进行了探究.请补充完整:
的图像与性质进行了探究.请补充完整:
(1)先填表,再在如图所示的平面直角坐标系中,描全表中各对对应值为坐标的点,并画出该函数的图像:
x | … | -5 | -4 | -3 | -2 | 0 | 1 | 2 | 3 | … |
| … | 2 |
| 3 | -3 |
| 0 | … |
(2)结合函数的图像,说出两条不同类型的性质;
①________________________________;____________________________________.
②![]() 的图像是由
的图像是由![]() 的图像如何平移得到?
的图像如何平移得到?
___________________________________________.
(3)当函数值![]() 时,x的取值范围是____________span>.
时,x的取值范围是____________span>.
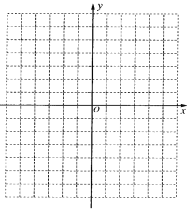
【答案】(1)5,1;(2)函数图像为双曲线,关于点(-1,1)中心对称;函数图像在每一支曲线上,y随x增大而增大;(3)向左平移一个单位,再向上平移一个单位;(4)x<-1或x>1
【解析】
通过表格画出图象,根据对称性填写表格即可;
(2)①填写对称性和增减性即可;②根据口诀”左加右减,上加下减”判断即可;
(3)根据图象写出范围即可.
(1)根据表格数据画出图象,并根据反比例规律填写表格.
如下表,如下图:
x | … | -5 | -4 | -3 | -2 | 0 | 1 | 2 | 3 | … |
| … | 2 |
| 3 | 5 | -3 | -1 |
| 0 | … |

(2)根据反比例的图象性质填写:
①函数图像为双曲线,关于点(-1,1)中心对称;函数图像在每一支曲线上,y随x增大而增大.
② ![]() 的图像是由
的图像是由![]() 的图像向左平移一个单位,再向上平移一个单位得到.
的图像向左平移一个单位,再向上平移一个单位得到.
(3)由图象可以看出函数值>﹣1,x的取值范围是x<-1或x>1.

 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案【题目】利民商场经营某种品牌的T恤,购进时的单价是300元,根据市场调查:在一段时间内,销售单价是400元时,销售量是60件,销售单价每涨10元,销售量就减少1件.设这种T恤的销售单价为x元(x>400)时,销售量为y件、销售利润为W元.
(1)请分别用含x的代数式表示y和W(把结果填入下表):
销售单价(元) | x |
销售量y(件) | |
销售利润W(元) |
(2)该商场计划实现销售利润10000元,并尽可能增加销售量,那么x的值应当是多少?