Question

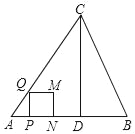
【题目】如图，已知在正方形ABCD中，F是CD边上一点（不与C、D重合），过点D作DG⊥BF交BF延长线于点G．连接AG，交BD于点E，交CD于点M，连接EF．若DG=4，AG=，则EF的长为____________．

Answer 1

【答案】

【解析】试题分析：

如图作AH⊥BG于H交BC于T，AN⊥GD于N，取BD的中点O，连接OA、OG．

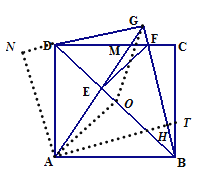
∴∠BAD＝∠BGD＝90°，

∴OA＝OD＝OB＝OG，

∴A、B、G、D四点共圆，

∴∠AGB＝∠ADB＝45°，∠AGD＝∠ABD＝45°，

∴AH＝GH，AN＝NG，

∵∠N＝∠AHG＝∠HGN＝90°，

∴四边形ANGH是矩形，∵AH＝HG，

∴四边形ANGH是正方形，

∵AG＝，

∴AH＝HG＝GN＝AN＝5，

易证△AND≌△AHB，

∴DN＝BH，

∴GD＋GB＝GN－DN＋GH＋BH＝2GN＝10，

∴4＋GB＝10，

∴GB＝6，BD＝＝＝，

∴BH＝1，

∵△BHT∽△AHB，

∴BH2＝AHHT，

∴HT＝，

∴AT＝AH＋TH＝，

易证△ABT≌△BCF，

∴AT＝BF＝，

∵△BEF∽△BGD，

∴，

∴，

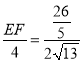∴EF＝ ．

故答案为．