��Ŀ����
����Ŀ����2016�㽭ʡ�����У���֪���κ���![]() ��ͼ����ͼ��ʾ
��ͼ����ͼ��ʾ
��1�����ݷ��̵ĸ��뺯��ͼ��֮��Ĺ�ϵ��������![]() �ĸ���ͼ�Ͻ��Ƶر�ʾ��������㣩�����۲�ͼ��д������
�ĸ���ͼ�Ͻ��Ƶر�ʾ��������㣩�����۲�ͼ��д������![]() �ĸ�����ȷ��0.1����
�ĸ�����ȷ��0.1����
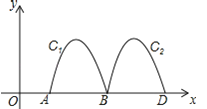
��2����ͬһֱ������ϵ�л���һ�κ���![]() ��ͼ�۲�ͼ��д���Ա���xȡֵ��ʲô��Χʱ��һ�κ�����ֵС�ڶ��κ�����ֵ��
��ͼ�۲�ͼ��д���Ա���xȡֵ��ʲô��Χʱ��һ�κ�����ֵС�ڶ��κ�����ֵ��
��3����ͼ����P������ƽ���ϵ�һ�㣬��������ĸ���ϣ���ѡ��һ���ʵ���ƽ�Ʒ�����ʹƽ�ƺ���κ���ͼ��Ķ�������P���ϣ�д��ƽ�ƺ���κ���ͼ��ĺ�������ʽ�����жϵ�P�Ƿ��ں���![]() ��ͼ���ϣ���˵�����ɣ�
��ͼ���ϣ���˵�����ɣ�

���𰸡���1��![]() ����1.6��
����1.6�� ![]() ��0.6����2����x����1.5��x��1ʱ����3��
��0.6����2����x����1.5��x��1ʱ����3��![]() ���ڣ�
���ڣ�
�����������⣨1����y=0�����������x�Ľ������꣬�Ӷ���ȷ����1����λ���ȵ���С�����α߳���4������������ֱ��y=1���ҳ�ֱ��y=1�������ߵĽ��㣬ֱ���������ߵĽ���ĺ����꼴�ɷ��̵Ľ⣻
��2�������ֱ����������������꣬Ȼ�����������ֱ���ɵõ�ֱ��![]() �ĺ���ͼ��Ȼ���ҳ�һ�κ���ͼ��λ��ֱ���·�����x��ȡֵ��Χ���ɣ�
�ĺ���ͼ��Ȼ���ҳ�һ�κ���ͼ��λ��ֱ���·�����x��ȡֵ��Χ���ɣ�
��3�������������ߵĶ�������͵�P�����꣬ȷ�����������ƶ��ķ���;��룬Ȼ�����������ߵĶ���ʽд�������ߵĽ���ʽ���ɣ�����P��������뺯������ʽ�������P��������Ϻ�������ʽ�����P��ֱ���ϣ������P����ֱ���ϣ�
�����������1������y=0�ã� ![]() ����ã�
����ã� ![]() ��
�� ![]() ������������x��Ľ�������Ϊ��0��0��������1��0����
������������x��Ľ�������Ϊ��0��0��������1��0����
��ֱ��y=1������������A��B���㣬�ֱ��A��B���㣬��AC��x�ᣬ����ΪC��BD��x�ᣬ����ΪD����C�͵�D�ĺ����꼴Ϊ���̵ĸ���
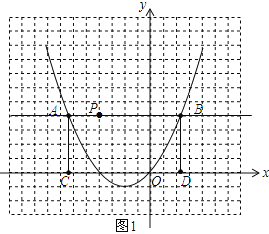
����ͼ�ο�֪���̵Ľ�Ϊ![]() ����1.6��
����1.6�� ![]() ��0.6��
��0.6��
��2���߽�x=0����![]() ��y=
��y=![]() ����x=1����ã�y=2����ֱ��
����x=1����ã�y=2����ֱ��![]() �����㣨0��
�����㣨0�� ![]() ������1��2����ֱ��
������1��2����ֱ��![]() ��ͼ����ͼ��ʾ��
��ͼ����ͼ��ʾ��
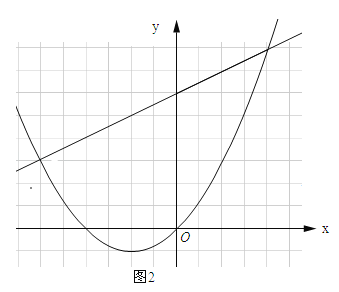
�ɺ���ͼ���֪����x����1.5��x��1ʱ��һ�κ�����ֵС�ڶ��κ�����ֵ��
��3��������ƽ��![]() ����λ��������ƽ��
����λ��������ƽ��![]() ����λ��ƽ�ƺ�Ķ�������ΪP����1��1����
����λ��ƽ�ƺ�Ķ�������ΪP����1��1����
ƽ�ƺ�ı���ʽΪy=��x+1��2+1����![]() ��
��
��P��![]() �ĺ���ͼ���ϣ�
�ĺ���ͼ���ϣ�
���ɣ��߰�x=��1�����y=1�����P���������ֱ�ߵĽ���ʽ�����P��ֱ��![]() �ĺ���ͼ���ϣ�
�ĺ���ͼ���ϣ�