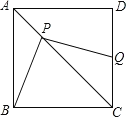
题目内容
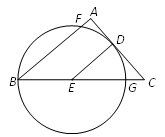
【题目】如图,在Rt△ABC中,∠A=90°,点D,E分别在AC,BC上,且CD·BC=AC·CE,以E为圆心,DE长为半径作圆,⊙E经过点B,与AB,BC分别交于点F,G.
(1)求证:AC是⊙E的切线;
(2)若AF=4,CG=5,
①求⊙E的半径;
②若Rt△ABC的内切圆圆心为I,则IE= .
【答案】(1)证明见解析;(2)①⊙E的半径为20;②IE=![]()
【解析】试题分析:(1)证明△CDE∽△CAB,得∠EDC=∠A=90°,所以AC是⊙E的切线;
(2)①如图1,作辅助线,构建矩形AHED,设⊙E的半径为r,表示BH和EC的长,证明△BHE∽△EDC,
列比例式代入r可得结论;
②如图2,作辅助线,构建直角△IME,分别求IM和ME的值,利用勾股定理可求IE的长.
试题解析:(1)∵CDBC=ACCE,
∴![]() ,
,
∵∠DCE=∠ACB,
∴△CDE∽△CAB,
∴∠EDC=∠A=90°,
∴ED⊥AC,
∵点D在⊙E上,
∴AC是⊙E的切线;
(2)①如图1,过E作EH⊥AB于H,
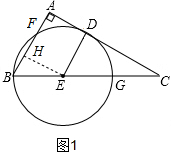
∴BH=FH,
∵∠A=∠AHE=∠ADE=90°,
∴四边形AHED是矩形,
∴ED=AH,ED∥AB,
∴∠B=∠DEC,
设⊙E的半径为r,则EB=ED=EG=r,
∴BH=FH=AH-AF=DE-AF=r-4,
EC=EG+CG=r+5,
在△BHE和△EDC中,
∵∠B=∠DEC,∠BHE=∠EDC=90°,
∴△BHE∽△EDC,
∴![]() ,即
,即![]() ,
,
∴r=20,
∴⊙E的半径为20;
②如图2,过I作IM⊥BC于M,过I作IH⊥AB于H,
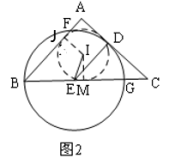
由①得:FH=BH=r-4=20-4=16,AB=AF+2BH=4+2×16=36,
BC=2r+5=2×20+5=45,
∴AC=![]() =27,
=27,
∵I是Rt△ABC的内心,
∴IM=![]() =9,
=9,
∴AH=IM=9,
∴BH=BM=36-9=27,
∴EM=27-20=7,
在Rt△IME中,由勾股定理得:IE=![]() .
.