Question

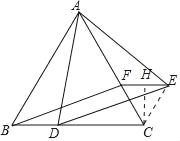
【题目】如图，已知△ABC是边长为3的等边三角形，点D是边BC上的一点，且BD＝1，以AD为边作等边△ADE，过点E作EF∥BC，交AC于点F，连接BF，则下列结论中①△ABD≌△BCF；②四边形BDEF是平行四边形；③S四边形BDEF＝；④S△AEF＝．其中正确的有(　　)

A. 1个B. 2个C. 3个D. 4个

Answer 1

【答案】C

【解析】

连接EC，作CH⊥EF于H．首先证明△BAD≌△CAE，再证明△EFC是等边三角形即可解决问题；

连接EC，作CH⊥EF于H．

∵△ABC，△ADE都是等边三角形，

∴AB＝AC，AD＝AE，∠BAC＝∠DAE＝∠ABC＝∠ACB＝60°，

∴∠BAD＝∠CAE，

∴△BAD≌△CAE，

∴BD＝EC＝1，∠ACE＝∠ABD＝60°，

∵EF∥BC，

∴∠EFC＝∠ACB＝60°，

∴△EFC是等边三角形，CH＝，

∴EF＝EC＝BD，∵EF∥BD，

∴四边形BDEF是平行四边形，故②正确，

∵BD＝CF＝1，BA＝BC，∠ABD＝∠BCF，

∴△ABD≌△BCF，故①正确，

∵S平行四边形BDEF＝BDCH＝，

故③正确，

∵△ABC是边长为3的等边三角形，S△ABC＝

∴S△ABD

∴S△AEF＝ S△AEC＝S△ABD＝

故④错误，

故选：C．