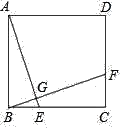
题目内容
【题目】在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 是射线
是射线![]() 上一点,
上一点,![]() 于点
于点![]() ,且
,且![]() ,连接
,连接![]() ,作
,作![]() 于点
于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
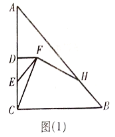

(1)如图(1),当点![]() 在线段
在线段![]() 上时,判断
上时,判断![]() 和
和![]() 的数量关系,并加以证明;
的数量关系,并加以证明;
(2)如图(2),当点![]() 在线段
在线段![]() 的延长线上时,问题(1)中的结论是否依然成立?如果成立,请求出当
的延长线上时,问题(1)中的结论是否依然成立?如果成立,请求出当![]() 和
和![]() 面积相等时,点
面积相等时,点![]() 与点
与点![]() 之间的距离;如果不成立,请说明理由.
之间的距离;如果不成立,请说明理由.
【答案】(1)![]() ,证明见解析;(2)依然成立,点
,证明见解析;(2)依然成立,点![]() 与点
与点![]() 之间的距离为
之间的距离为![]() .理由见解析.
.理由见解析.
【解析】
(1)做辅助线,通过已知条件证得![]() 与
与![]() 是等腰直角三角形.证出
是等腰直角三角形.证出![]() ,利用全等的性质即可得到
,利用全等的性质即可得到![]() .
.
(2)设AH,DF交于点G,可根据ASA证明△FCE≌△HFG,从而得到![]() ,当
,当![]() 和
和![]() 均为等腰直角三角形当他们面积相等时,
均为等腰直角三角形当他们面积相等时,![]() .利用勾股定理可以求DE、CE的长,即可求出CE的长,即可求得点
.利用勾股定理可以求DE、CE的长,即可求出CE的长,即可求得点![]() 与点
与点![]() 之间的距离.
之间的距离.
(1)![]()
证明:延长![]() 交
交![]() 于点
于点![]()
∵在![]() 中,
中,![]() ,
,![]() ,
,
∴![]()
∵![]() 于点
于点![]() ,且
,且![]() ,
,
∴![]() ,
,![]() 与
与![]() 是等腰直角三角形.
是等腰直角三角形.
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵点![]() 是
是![]() 的中点,∴
的中点,∴![]() ,∴
,∴![]()
∴![]()
∵![]() 于点
于点![]() ,∴
,∴![]() ,∴
,∴![]()
∴![]()
∴![]()
∴![]() ;
;
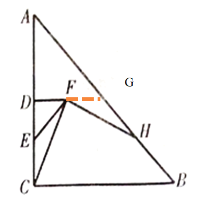
(2)依然成立
理由:设AH,DF交于点G,
由题意可得出:DF=DE,
∴∠DFE=∠DEF=45°,
∵AC=BC,
∴∠A=∠CBA=45°,
∵DF∥BC,
∴∠CBA=∠FGB=45°,
∴∠FGH=∠CEF=45°,
∵点D为AC的中点,DF∥BC,
∴DG=![]() BC,DC=
BC,DC=![]() AC,
AC,
∴DG=DC,
∴EC=GF,
∵∠DFC=∠FCB,
∴∠GFH=∠FCE,
在△FCE和△HFG中
 ,
,
∴△FCE≌△HFG(ASA),
∴HF=FC.
由(1)可知![]() 和
和![]() 均为等腰直角三角形
均为等腰直角三角形
当他们面积相等时,![]() .
.
∴![]()
∴![]()
∴点![]() 与点
与点![]() 之间的距离为
之间的距离为![]() .
.

练习册系列答案
相关题目