题目内容
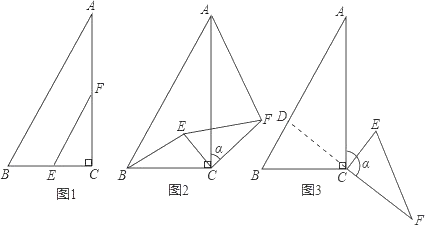
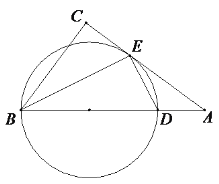
【题目】如图,Rt△ABC中,∠C=90°,∠B的平分线交AC于E,DE⊥BE.
(1)试说明AC是△BED外接圆的切线;
(2)若CE=1,BC=2,求△ABC内切圆的面积.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)根据圆周角定理即可证得BD是外接圆的直径,则作出BD的中点就是圆的圆心,连接OE,证明OE⊥AC即可证得AC是切线;
(2)求出AB、AC,根据Rt△ABC的内切圆的半径r= ![]() ,计算即可;
,计算即可;
(1)证明:作BD的中点O,连接OE.
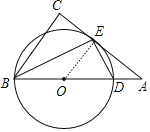
∵DE⊥BE,
∴BD是圆的直径.
∵OB=OE,
∴∠EBO=∠BEO,
又∵∠CBE=∠EBO,
在直角△BCE中,∠CBE+∠CEB=90°,
∴∠CEB+∠BEO=90°,即∠CEO=90°.
∴OE⊥AC,
∴AC是△BED外接圆的切线;
(2)解:在Rt△BCE中,BE= ![]() ,
,
∵∠CBE=∠DBE,∠C=∠BED=90°,
∴△CBE∽△EBD,
∴![]() ,
,
∴![]() ,
,
∴DE= ![]() ,BD=
,BD= ![]() ,
,
∵OE∥BC,
∴![]() ,
,
∴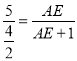 ,
,
∴AE= ![]() ,
,
∴![]() ,
,
∴OA= ![]() ,
,
∴AB= ![]() ,AC=
,AC= ![]() ,
,
∵△ABC是直角三角形,
∴△ABC的内切圆的半径r=![]() =
= ![]()
∴圆的面积是:π![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】某厂家销售一种产品,现准备从网上销售和市场直销两种销售方案中选择一种进行销售.由于受各种不确定因素影响,不同销售的方案会产生不同的成本和其它费用.设每月销售x件,网上销售月利润为w网(元),市场直销月利润为w市(元),具体信息如表:
每件售价(元) | 每件成本(元) | 月其他费用(元) | |
网上销售 | - | 20 | 45000 |
市场直销 | 120 | k |
|
其中k为常数,且30≤k≤50.月利润=月销售额-月成本-月其它费用.
(1)当x=500时,网上销售单价为______元.
(2)分别求出w网,w市与x间的函数解析式(不必写x的取值范围).
(3)若网上销售月利润的最大值与市场直销月利润的最大值相同,求k的值.
(4)如果某月要将3000件产品全部销售完,请你通过分析帮厂家做出决策,选择在网上销售还是市场直销才能使月利润较大?