题目内容
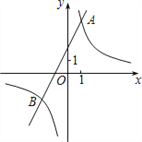
【题目】如图,在四边形ABCD中,AB∥CD,∠ABC=∠ADC,DE垂直于对角线AC,垂足是E,连接BE. 
(1)求证:四边形ABCD是平行四边形;
(2)若AB=BE=2,sin∠ACD= ![]() ,求四边形ABCD的面积.
,求四边形ABCD的面积.
【答案】
(1)证明:∵AB∥CD,
∴∠ABC+∠DCB=180°,
∵∠ABC=∠ADC,
∴∠ADC+∠BCD=180°,
∴AD∥BC,
∵AB∥CD,
∴四边形ABCD是平行四边形
(2)解:∵sin∠ACD= ![]() ,
,
∴∠ACD=60°,
∵四边形ABCD是平行四边形,
∴AB∥CD,CD=AB=2,
∴∠BAC=∠ACD=60°,
∵AB=BE=2,
∴△ABE是等边三角形,
∴AE=AB=2,
∵DE⊥AC,
∴∠CDE=90°﹣60°=30°,
∴CE= ![]() CD=1,
CD=1,
∴DE= ![]() CE=
CE= ![]() ,AC=AE+CE=3,
,AC=AE+CE=3,
∴平行四边形ABCD的面积=2△ACD的面积=ACDE=3 ![]()
【解析】(1)根据平行四边形的性质得出∠ABC+∠DCB=180°,推出∠ADC+∠BCD=180°,根据平行线的判定得出AD∥BC,根据平行四边形的判定推出即可;(2)证明△ABE是等边三角形,得出AE=AB=2,由直角三角形的性质求出CE和DE,得出AC的长,即可求出四边形ABCD的面积.
【考点精析】利用平行四边形的判定与性质和解直角三角形对题目进行判断即可得到答案,需要熟知若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).

【题目】列方程解应用题
四川的灾情牵动全国人民的心,某市A、B两个蔬菜基地得知四川C、D两个灾民安置点分别急蔬菜240吨和260吨的消息后,决定调运蔬菜支援灾区。已知A蔬菜基地有蔬菜200吨,B蔬菜基地有蔬菜300吨,现将这些蔬菜全部调往C、D两个灾民安置点。从A地运往C、D两处的费用分别为每吨20元和25元,从B地运往C、D两处的费用分别为每吨15元和18元。设从B地运往C处的蔬菜为![]() 吨。
吨。
(1)请填写下表,并求两个蔬菜基地调运蔬菜的运费相等时![]() 的值?
的值?
C | D | 总计 | |
A | 200吨 | ||
B |
| 300吨 | |
总计 | 240吨 | 260吨 | 500吨 |
(2)已知总运费最小的调运费用是9280元,请你提交具体的调运方案.