题目内容
【题目】某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),已知计划中的建筑材料可建围墙的总长为为50m.设饲养室长为x(m),占地面积为y(m2).
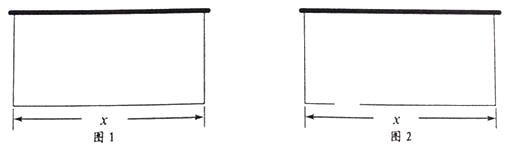
(1)如图1,问饲养室长x为多少时,占地面积y最大?
(2)如图2,现要求在图中所示位置留2m宽的门,且仍使饲养室的占地面积最大。小敏说:“只要饲养室长比(1)中的长多2m就行了.”
【答案】
(1)
解:因为 ![]() ,
,
所以当x=25时,占地面积y最大,
即当饲养室长为25m时,占地面积最大.
(2)
解:因为 ![]() ,
,
所以当x=26时,占地面积y最大,
即饲养室长为26m时,占地面积最大.
因为26-25=1≠2,
所以小敏的说法不正确.
【解析】(1)根据矩形的面积=长×高,已知长为x,则宽为 ![]() ,代入求出y关于x的函数解析式,配成二次函数的顶点式,即可求出x的值时,y有最大值;(2)长虽然不变,但长用料用了(x-2)m,所以宽变成了
,代入求出y关于x的函数解析式,配成二次函数的顶点式,即可求出x的值时,y有最大值;(2)长虽然不变,但长用料用了(x-2)m,所以宽变成了 ![]() ,由(1)同理,代入求出y关于x的函数解析式,配成二次函数的顶点式,即可求出x的值时,y有最大值.
,由(1)同理,代入求出y关于x的函数解析式,配成二次函数的顶点式,即可求出x的值时,y有最大值.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
【题目】将从1开始的连续自然数按图规律排列:规定位于第m行,第n列的自然数10记为(3,2),自然数15记为(4,2)…
列 行 | 第1列 | 第2列 | 第3列 | 第4列 |
第1行 | 1 | 2 | 3 | 4 |
第2行 | 8 | 7 | 6 | 5 |
第3行 | 9 | 10 | 11 | 12 |
第4行 | 16 | 15 | 14 | 13 |
… | … | … | … | … |
第n行 | … | … | … | … |
按此规律,回答下列问题:
(1)记为(6,3)表示的自然数是__________________.
(2)自然数2018记为_________________.
(3)用一个正方形方框在第span>3列和第4列中任意框四个数,这四个数的和能为2018吗?如果能,求出框出的四个数中最小的数;如果不能,请写出理由。