题目内容
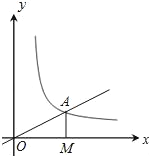
【题目】如图,正比例函数y=![]() x的图象与反比例函数y=
x的图象与反比例函数y=![]() (k≠0)在第一象限的图象交于A点,过A点作x轴的垂线AM,垂足为M,已知△OAM的面积为1.
(k≠0)在第一象限的图象交于A点,过A点作x轴的垂线AM,垂足为M,已知△OAM的面积为1.
(1)求反比例函数的解析式;
(2)求点A的坐标;
(3)如果B为反比例函数在第一象限图象上的点(点B与点A不重合),且B点的横坐标为1,在x轴上确定一点P,使PA+PB最小.求点P的坐标.
【答案】(1)反比例函数的解析式为y=![]() .(2)P点的坐标为(
.(2)P点的坐标为(![]() ,0).
,0).
【解析】试题分析:(1)设点A的坐标为(a,b),由点A在反比例函数图象上结合三角形△OAM的面积为1,可得出关于k、a、b的三元一次方程组,解方程即可求出k值,从而得出反比例函数解析式;
(2)联立直线与反比例函数解析式求出点A的坐标,找出点A关于x轴的对称点C的坐标,再结合反比例函数解析式求出点B坐标,连接BC即可找出点P的位置,由点B、C的坐标利用待定系数法即可求出直线BC的解析式,令y=0求出x值即可得出点P的坐标.
试题解析:(1)设点A的坐标为(a,b),
则 ,解得:k=2.
,解得:k=2.
∴反比例函数的解析式为y=![]() .
.
(2)联立直线OA和反比例函数解析式得:
 ,解得:
,解得:![]() .
.
∴点A的坐标为(2,1).
设A点关于x轴的对称点为C,则C点的坐标为(2,-1),连接BC较x轴于点P,点P即为所求.如图所示.

设直线BC的解析式为y=mx+n,
由题意可得:B点的坐标为(1,2),
∴![]() ,解得:
,解得:![]() .
.
∴BC的解析式为y=-3x+5.
当y=0时,0=-3x+5,解得:x=![]() .
.
∴P点的坐标为(![]() ,0).
,0).

【题目】为了进一步了解某校八年级学生的身体素质情况,体育老师对该校八年级(1)班50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,图表如下所示:
组别 | 次数x | 频数(人数) |
第1组 | 80≤x<100 | 6 |
第2组 | 100≤x<120 | 8 |
第3组 | 120≤x<140 | a |
第4组 | 140≤x<160 | 18 |
第5组 | 160≤x<180 | 6 |
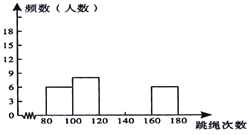
请结合图表完成下列问题:
(1)求表中a的值并把频数分布直方图补充完整;
(2)该班学生跳绳的中位数落在第 组,众数落在第 组;
(3)若在一分钟内跳绳次数少于120次的为测试不合格,则该校八年级共1000人中,一分钟跳绳不合格的人数大约有多少?