题目内容
【题目】我们可用![]() 表示以
表示以![]() 为自变量的函数,如一次函数
为自变量的函数,如一次函数![]() ,可表示为
,可表示为![]() ,且
,且![]() ,
,![]() ,定义:若存在实数
,定义:若存在实数![]() ,使
,使![]() 成立,则称
成立,则称![]() 为
为![]() 的不动点,例如:
的不动点,例如:![]() ,令
,令![]() ,得
,得![]() ,那么
,那么![]() 的不动点是1.
的不动点是1.
(1)已知函数![]() ,求
,求![]() 的不动点.
的不动点.
(2)函数![]() (
(![]() 是常数)的图象上存在不动点吗?若存在,请求出不动点;若不存在,请说明理由;
是常数)的图象上存在不动点吗?若存在,请求出不动点;若不存在,请说明理由;
(3)已知函数![]() (
(![]() ),当
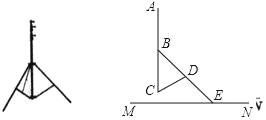
),当![]() 时,若一次函数
时,若一次函数![]() 与二次函数
与二次函数![]() 的交点为
的交点为![]() ,即
,即![]() 两点的横坐标是函数
两点的横坐标是函数![]() 的不动点,且
的不动点,且![]() 两点关于直线
两点关于直线![]() 对称,求
对称,求![]() 的取值范围.
的取值范围.
【答案】(1![]() 的不动点为0和2;(2)①
的不动点为0和2;(2)①![]() 时,有唯一的不动点
时,有唯一的不动点![]() ②
②![]() 时,有无数个不动点③
时,有无数个不动点③![]() 时,没有不动点;(3)
时,没有不动点;(3)![]() 的取值范围是
的取值范围是![]()
【解析】
(1)根据不动点的性质即可列方程求解;
(2)令![]() ,得:
,得:![]() ,根据m,n的取值进行讨论即可求解;
,根据m,n的取值进行讨论即可求解;
(3)令![]() ,则
,则![]() ,根据一元二次方程根与系数求出A,B的中点C的坐标,再根据点
,根据一元二次方程根与系数求出A,B的中点C的坐标,再根据点![]() 在直线
在直线![]() 上,得到
上,得到![]() ,得到b关于a的二次函数,再根据二次函数的性质即可求解.
,得到b关于a的二次函数,再根据二次函数的性质即可求解.
解:(1)令![]() ,则
,则![]() ,
,![]() ,
,![]()
所以![]() 的不动点为0和2
的不动点为0和2
(2)令![]() ,得:
,得:![]()
![]()
①若![]() ,即
,即![]() 时,有唯一的不动点
时,有唯一的不动点![]()
②若![]() ,
,![]() ,即
,即![]() 时,有无数个不动点
时,有无数个不动点
③若![]() ,即
,即![]() 时,没有不动点
时,没有不动点
(3)令![]() ,则
,则![]()
设![]() ,
,![]() ,则
,则![]() ,
,![]()
![]() 的中点
的中点![]() 坐标为
坐标为![]()
![]() ,
,![]()
所以![]()
点![]() 在直线
在直线![]() 上,所以
上,所以![]()
![]()
当![]() 时,
时,![]()
此时,![]() 恒大于0
恒大于0
所以![]() 的取值范围是
的取值范围是![]()

【题目】某体育用品商场采购员要到厂家批发购买篮球和排球共![]() 个,篮球个数不少于排球个数,付款总额不得超过
个,篮球个数不少于排球个数,付款总额不得超过![]() 元,已知两种球厂的批发价和商场的零售价如下表. 设该商场采购
元,已知两种球厂的批发价和商场的零售价如下表. 设该商场采购![]() 个篮球.
个篮球.
品名 | 厂家批发价/元/个 | 商场零售价/元/个 |
篮球 |
|
|
排球 |
|
|
(1)求该商场采购费用![]() (单位:元)与
(单位:元)与![]() (单位:个)的函数关系式,并写出自变最
(单位:个)的函数关系式,并写出自变最![]() 的取值范围:
的取值范围:
(2)该商场把这![]() 个球全都以零售价售出,求商场能获得的最大利润;
个球全都以零售价售出,求商场能获得的最大利润;
(3)受原材料和工艺调整等因素影响,采购员实际采购时,低球的批发价上调了![]() 元/个,同时排球批发价下调了
元/个,同时排球批发价下调了![]() 元/个.该体有用品商场决定不调整商场零售价,发现将
元/个.该体有用品商场决定不调整商场零售价,发现将![]() 个球全部卖出获得的最低利润是
个球全部卖出获得的最低利润是![]() 元,求
元,求![]() 的值.
的值.