题目内容
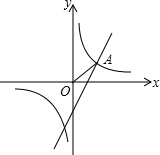
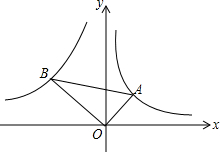
如图，已知第一象限内的点A在反比例函数y=
的图象上，第二象限内的点B在反比例函数y=
的图象上，且OA⊥OB，tanA=
，则k的值为（ ）
| 2 |
| x |
| k |
| x |
| 3 |
| A．-3 | B．-
| C．-6 | D．-2
|
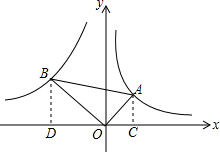
作AC⊥x轴于点C，作BD⊥x轴于点D．
则∠BDO=∠ACO=90°，
则∠BOD+∠OBD=90°，
∵OA⊥OB，
∴∠BOD+∠AOC=90°，
∴∠BOD=∠AOC，
∴△OBD∽△AOC，
∴
=（
）2=（tanA）2=3，
又∵S△AOC=
×2=1，
∴S△OBD=3，
∴k=-6．
故选C．
则∠BDO=∠ACO=90°，
则∠BOD+∠OBD=90°，
∵OA⊥OB，
∴∠BOD+∠AOC=90°，
∴∠BOD=∠AOC，
∴△OBD∽△AOC，
∴
| S△OBD |
| S△AOC |
| OB |
| OA |
又∵S△AOC=
| 1 |
| 2 |
∴S△OBD=3，
∴k=-6．
故选C．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
