题目内容
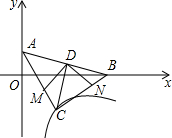
如图,不重合的A(2,n)、B(n,2)两点在y=
(x>0)反比例函数的图象上,BC垂直于y轴于点C.
(1)求n的值;
(2)判断△ABC的形状;
(3)若存在点P(m,0),使△PAB是直角三角形,求出满足条件的所有m的值.

| n+4 |
| x |
(1)求n的值;
(2)判断△ABC的形状;
(3)若存在点P(m,0),使△PAB是直角三角形,求出满足条件的所有m的值.

(1)把A(2,n)代入y=
(x>0)得:2n=n+4,
解得:n=4;
(2)△ABC为等腰直角三角形,理由为:
过A作AE⊥x轴,交BC于点D,
由(1)可知:A(2,4),B(4,2),
∵BC⊥y轴于点C,
∴点C(0,2),
∴CD=BD=AD=DE=2,
∴△ACD与△ABD都为等腰直角三角形,
∴∠CAD=∠BAD=45°,即∠CAB=90°,
∵AC=AB=2
,
∴△ABC为等腰直角三角形;
(3)连接BE,
∵AD=DE=BD=2,BD⊥AE,
∴△ABD与△BDE都为等腰直角三角形,即∠ABD=∠EBD=45°,
∴∠ABE=90°,AB=BE=2
,
则当P与E重合时,△PAB为直角三角形,此时P坐标为(2,0);
延长AC与x轴交于点P,连接PB,此时∠PAB=90°,△PAB为直角三角形,
设直线AC解析式为y=kx+b,
将A与C坐标代入得:
,
解得:
,
∴直线AC解析式为y=x+2,
令y=0,求得:x=-2,即P(-2,0),
综上,m的值为2或-2.
| n+4 |
| x |
解得:n=4;
(2)△ABC为等腰直角三角形,理由为:
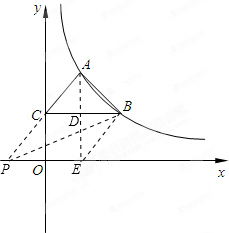
过A作AE⊥x轴,交BC于点D,
由(1)可知:A(2,4),B(4,2),
∵BC⊥y轴于点C,
∴点C(0,2),
∴CD=BD=AD=DE=2,
∴△ACD与△ABD都为等腰直角三角形,
∴∠CAD=∠BAD=45°,即∠CAB=90°,
∵AC=AB=2
| 2 |
∴△ABC为等腰直角三角形;
(3)连接BE,
∵AD=DE=BD=2,BD⊥AE,
∴△ABD与△BDE都为等腰直角三角形,即∠ABD=∠EBD=45°,
∴∠ABE=90°,AB=BE=2
| 2 |
则当P与E重合时,△PAB为直角三角形,此时P坐标为(2,0);
延长AC与x轴交于点P,连接PB,此时∠PAB=90°,△PAB为直角三角形,
设直线AC解析式为y=kx+b,
将A与C坐标代入得:
|
解得:
|
∴直线AC解析式为y=x+2,
令y=0,求得:x=-2,即P(-2,0),
综上,m的值为2或-2.


练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
 时间t的关系如图所示:
时间t的关系如图所示: