ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ»γΆΦΔΌΓΔΆΦΔΎΘ§‘ΎΗχΕ®ΒΡ“Μ’≈ΨΊ–Έ÷ΫΤ§…œΉς“ΜΗω’ΐΖΫ–ΈΘ§ΦΉΓΔ““ΝΫ»ΥΒΡΉςΖ®»γœ¬ΘΚ
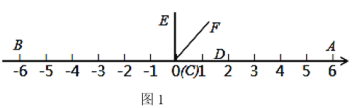
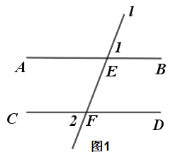
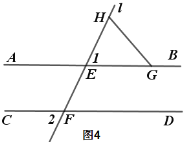
ΦΉΘΚ“‘ΒψAΈΣ‘≤–ΡΘ§AD≥ΛΈΣΑκΨΕΜ≠ΜΓΘ§ΫΜAB”ΎΒψEΘ§“‘ΒψDΈΣ‘≤–ΡΘ§AD≥ΛΈΣΑκΨΕΜ≠ΜΓΘ§ΫΜCD”ΎΒψFΘ§Ν§Ϋ”EFΘ§‘ρΥΡ±Ώ–ΈAEFDΦ¥ΈΣΥυ«σΘΜ
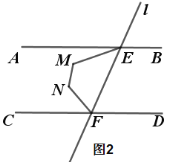
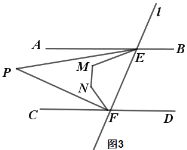
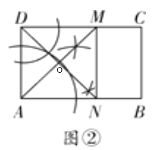
““ΘΚΉςΓœDABΒΡΤΫΖ÷œΏΘ§ΫΜCD”ΎΒψMΘ§Ά§άμΉςΓœADCΒΡΤΫΖ÷œΏΘ§ΫΜAB”ΎΒψNΘ§Ν§Ϋ”MNΘ§‘ρΥΡ±Ώ–ΈADMNΦ¥ΈΣΥυ«σΘ°


Ε‘”Ύ“‘…œΝΫ÷÷ΉςΖ®Θ§Ω…“‘Ήω≥ωΒΡ≈–Ε® «(ΓΓΓΓ)
A.ΦΉ’ΐ»ΖΘ§““¥μΈσB.ΦΉΓΔ““Ψυ’ΐ»Ζ
C.““’ΐ»ΖΘ§ΦΉ¥μΈσD.ΦΉΓΔ““Ψυ¥μΈσ
ΓΨ¥πΑΗΓΩB
ΓΨΫβΈωΓΩ
”…“ΜΉιΝΎ±ΏœύΒ»ΒΡΨΊ–Έ «’ΐΖΫ–ΈΩ…÷ΣΦΉ’ΐ»ΖΘ§”…Ε‘Ϋ«œΏΜΞœύ¥Ι÷±ΤΫΖ÷«“œύΒ»ΒΡΥΡ±Ώ–Έ «’ΐΖΫ–ΈΩ…÷Σ““’ΐ»Ζ.
ΫβΘΚ”…ΦΉΒΡΉςΆΦΩ…÷Σ![]() Θ§
Θ§![]() Θ§
Θ§![]()
![]() ΥΡ±Ώ–ΈABCD «ΨΊ–Έ
ΥΡ±Ώ–ΈABCD «ΨΊ–Έ
![]()
![]() ΥΡ±Ώ–ΈAEFD «ΨΊ–Έ
ΥΡ±Ώ–ΈAEFD «ΨΊ–Έ
![]()
![]() ΥΡ±Ώ–ΈAEFD «’ΐΖΫ–ΈΘ§ΦΉ’ΐ»ΖΘΜ
ΥΡ±Ώ–ΈAEFD «’ΐΖΫ–ΈΘ§ΦΉ’ΐ»ΖΘΜ
»γΆΦΘ§AMΚΆDNΫΜ”ΎΒψOΘ§
![]() ΥΡ±Ώ–ΈABCD «ΨΊ–Έ
ΥΡ±Ώ–ΈABCD «ΨΊ–Έ
![]()
![]() «ΓœDABΒΡΤΫΖ÷œΏΘ§
«ΓœDABΒΡΤΫΖ÷œΏΘ§![]() «ΓœADCΒΡΤΫΖ÷œΏΘ§
«ΓœADCΒΡΤΫΖ÷œΏΘ§
![]() Θ§
Θ§![]()
![]()
![]() Θ§Φ¥
Θ§Φ¥![]() Θ§
Θ§
![]()
![]()
Ά§άμΩ…÷Λ![]()
![]()
![]() «“AMΚΆDNΜΞœύΤΫΖ÷
«“AMΚΆDNΜΞœύΤΫΖ÷
![]() ΥΡ±Ώ–ΈAEFD «’ΐΖΫ–ΈΘ§““’ΐ»Ζ.
ΥΡ±Ώ–ΈAEFD «’ΐΖΫ–ΈΘ§““’ΐ»Ζ.
Υυ“‘ΦΉ““ΒΡΨυ’ΐ»Ζ.
Ι ―ΓΘΚB.

ΓΨΧβΡΩΓΩΫώΡξΡξ≥θΘ§Έ“Ι汧ΖΔ–¬ΙΎΖΈ―Ή“Ώ«ιΘ§Ρ≥ ΓΝΎΫϋœΊ – CΓΔD Μώ÷Σ AΓΔB ΝΫ –Ζ÷±πΦ±–ηΨ»‘°ΈοΉ 200Ε÷ΚΆ 300 Ε÷ΒΡœϊœΔΚσΘ§ΨωΕ®Βς‘ΥΈοΉ ÷ß‘°Θ°“―÷Σ C –”–Ψ»‘°ΈοΉ 240 Ε÷Θ§D –”–Ψ»‘°ΈοΉ 260 Ε÷Θ§œ÷ΫΪ’β–©Ψ»‘°ΈοΉ »Ϊ≤ΩΒςΆυ AΓΔB ΝΫ –Θ°“―÷Σ¥” C –‘ΥΆυ AΓΔB ΝΫ –ΒΡΖ―”ΟΖ÷±πΈΣΟΩΕ÷ 20 ‘ΣΚΆ 25 ‘ΣΘ§¥”D –‘ΥΆυΆυ AΓΔB ΝΫ –ΒΡΖ―”ΟΖ÷±πΈΣΟΩΕ÷ 15 ‘ΣΚΆ 30 ‘ΣΘ§…η¥” C –‘ΥΆυ A –ΒΡΨ»‘°ΈοΉ ΈΣ x Ε÷Θ°
Θ®1Θ© «κΧν–¥œ¬±μΘΜ
A | B | ΚœΦΤΘ®Ε÷Θ© | |
C | x | _____ | 240 |
D | _____ | _____ | 260 |
ΉήΦΤΘ®Ε÷Θ© | 200 | 300 | 500 |
Θ®2Θ©…η CΓΔD ΝΫ –ΒΡΉή‘ΥΖ―ΈΣ W ‘ΣΘ§‘ρ W ”κ x ÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΈΣ_________Θ§Τδ÷–Ή‘±δΝΩ xΒΡ»Γ÷ΒΖΕΈß «________ΘΜ
Θ®3Θ©Ψ≠Ιΐ«ά–όΘ§¥” C –ΒΫ B –ΒΡ¬ΖΩωΒΟΒΫΝΥΗΡ…ΤΘ§ΥθΕΧΝΥ‘Υ δ ±ΦδΘ§‘ΥΖ―ΟΩΕ÷Φθ…Ό n ‘ΣΘ®nΘΨ10Θ©Θ§Τδ”ύ¬ΖœΏ‘ΥΖ―≤Μ±δΘ§»τ CΓΔD ΝΫ –ΒΡΉή‘ΥΖ―ΒΡΉν–Γ÷Β≤Μ–Γ”Ύ 7920 ‘ΣΘ§‘ρ n ΒΡ»Γ÷ΒΖΕΈß «______________Θ°