题目内容
【题目】如图,四边形ABCD中,AC、BD是它的对角线,∠ABC=∠ADC=90°,∠BCD是锐角.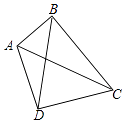
(1)写出这个四边形的一条性质并证明你的结论.
(2)若BD=BC,证明: ![]() .
.
(3)①若AB=BC=4,AD+DC=6,求 ![]() 的值.
的值.
②若BD=CD,AB=6,BC=8,求sin∠BCD的值.
【答案】
(1)
解:结论:AB2+BC2=AD2+DC2.
理由:∵∠ABC=∠ADC=90°,
∴AB2+BC2=AC2,BC2+DC2=AC2,
∴AB2+BC2=AD2+DC2
(2)
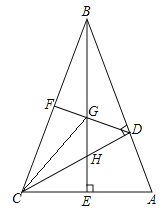
解:如图1中,过点B作AD的垂线BE交DA的延长线于点E,
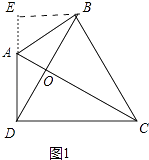
∵∠ABC=∠ADC=90°,
∴∠ADC+∠ABC=180°,
∴四边形ABCD四点共圆,
∴∠BDE=∠ACB,∠EAB=∠BCD,
∵∠BED=∠ABC=90°,
∴△BED∽△ABC,
∴ ![]() =
= ![]() =sin∠EAB=sin∠BCD
=sin∠EAB=sin∠BCD
(3)
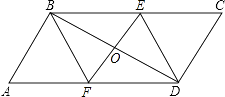
解:①如图2中,过点B作BF⊥BD交DC的延长线于F.
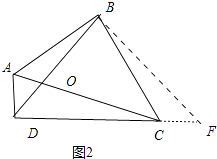
∵∠ABC=∠DBF=90°,∠BAD+∠BCD+∠ABC+∠ADC=360°,∠ABC+∠ADC=180°,
∴∠BAD=180°﹣∠BCD=∠BCF,
∵∠BCF=∠BAD,BC=BA,
∴△DAB≌△CBF,
∴BD=BF,AD=CF,
∵∠DBF=90°,
∴△BDF是等腰直角三角形,
∴BD= ![]() DF,
DF,
∵AD+CD=6,
∴CF+CD=DF=6,
∴BD=3 ![]() ,AC=
,AC= ![]() =4
=4 ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() .
.
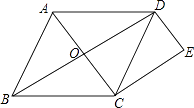
②当BD=CD时,如图3中,过点B作MN∥DC,过点C作CN⊥MN,垂足为NM延长BA交MN于点N,则四边形DCNM是矩形,△ABM∽△BCN,
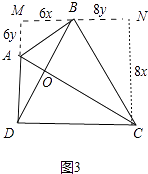
∴ ![]() ,设AM=6y,BN=8y,BM=6x,CN=8x,
,设AM=6y,BN=8y,BM=6x,CN=8x,
在Rt△BDM中,BD= ![]() =10x,
=10x,
∵BD=DC,
∴10x=6x+8y,
∴x=2y,
在Rt△DABM中,AB= ![]() =6
=6 ![]() y,
y,
∴sin∠BCD=sin∠MAB= ![]() =
= ![]() =
= ![]()
【解析】(1)结论:AB2+BC2=AD2+DC2 , 根据勾股定理即可证明.(2)如图1中,过点B作AD的垂线BE交DA的延长线于点E,只要证明△BED∽△ABC,即可解决问题.(3)①如图2中,过点B作BF⊥BD交DC的延长线于F.只要证明△DAB≌△CBF,推出DF=AD+CD=6,求出BD、AC即可.
②当BD=CD时,如图3中,过点B作MN∥DC,过点C作CN⊥MN,垂足为NM延长BA交MN于点N,则四边形DCNM是矩形,△ABM∽△BCN,所以 ![]() ,设AM=6y,BN=8y,BM=6x,CN=8x,通过BD=DC,列出方程求出x、y的关系,求出AB,即可解决问题.
,设AM=6y,BN=8y,BM=6x,CN=8x,通过BD=DC,列出方程求出x、y的关系,求出AB,即可解决问题.

 阅读快车系列答案
阅读快车系列答案