题目内容
【题目】如图,在平行四边形ABCD中,过对角线BD中点的直线交AD、BC边于F、E. 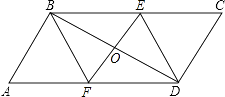
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,写出EF与BD的关系.
(3)若∠A=60°,AB=4,BC=6,四边形BEDF是矩形,求该矩形的面积.
【答案】
(1)解:∵四边形ABCD是平行四边形,O是BD中点,
∴BC∥AD,OB=OD,
∴∠OBE=∠ODF,
又∵∠BOE=∠DOF,
∴△BOE≌△DOF(ASA),
∴EO=FO,
∴四边形BEDF是平行四边形
(2)解:当四边形BEDF是菱形时,根据菱形的性质可得:EF与BD互相垂直平分
(3)解:∵四边形BEDF是矩形
∴∠AFB=90°
又∵∠A=60°,
∴∠ABF=30°,
∴AF= ![]() AB=
AB= ![]() ×4=2,
×4=2,
∴Rt△ABF中,BF=2 ![]() ,
,
又∵AD=BC=6,
∴DF=6﹣2=4,
∴矩形BEDF的面积=BF×DF=2 ![]() ×4=8
×4=8 ![]() .
.
【解析】(1)根据平行四边形ABCD的性质,判定△BOE≌△DOF(ASA),得出四边形BEDF的对角线互相平分,进而得出结论;(2)根据根据菱形的性质作出判断:EF与BD互相垂直平分;(3)根据Rt△ABF的边角关系,求得BF和AF,再根据矩形的性质,求得DF的长,最后计算矩形的面积.
【考点精析】掌握平行四边形的判定与性质和矩形的性质是解答本题的根本,需要知道若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积;矩形的四个角都是直角,矩形的对角线相等.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目