题目内容
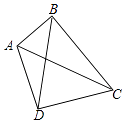
【题目】如图,已知菱形ABCD中,对角线AC、BD相交于点O,过点C作CE∥BD,过点D作DE∥AC,CE与DE相交于点E. 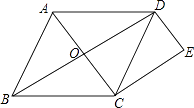
(1)求证:四边形CODE是矩形;
(2)若AB=5,AC=6,求四边形CODE的周长.
【答案】
(1)证明:如图,∵四边形ABCD为菱形,
∴∠COD=90°;而CE∥BD,DE∥AC,
∴∠OCE=∠ODE=90°,
∴四边形CODE是矩形
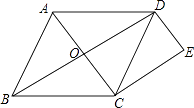
(2)解:∵四边形ABCD为菱形,
∴AO=OC= ![]() AC=3,OD=OB,∠AOB=90°,
AC=3,OD=OB,∠AOB=90°,
由勾股定理得:
BO2=AB2﹣AO2,而AB=5,
∴DO=BO=4,
∴四边形CODE的周长=2(3+4)=14
【解析】(1)如图,首先证明∠COD=90°;然后证明∠OCE=∠ODE=90°,即可解决问题.(2)如图,首先证明CO=AO=3,∠AOB=90°;运用勾股定理求出BO,即可解决问题.
【考点精析】根据题目的已知条件,利用菱形的性质和矩形的判定方法的相关知识可以得到问题的答案,需要掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案【题目】随着裕安中学的规模逐渐扩大,学生人数越来越多,学校打算购买校车20辆,现有A和B两种型号校车,如果购买A型号校车6辆,B型号14辆,需要资金580万元;如果购买A型号校车12辆,B型号校车8辆,需要资金760万元.已知每种型号校车的座位数如表所示:
A型号 | B型号 | |
座位数(个/辆) | 60 | 30 |
经预算,学校准备购买设备的资金不高于500万元.(每种型号至少购买1辆)
(1)每辆A型校车和B型校车各多少万元?
(2)请问学校有几种购买方案?且哪种方案的座位数最多,是多少?
【题目】为弘扬中华传统文化,某校组织八年级1000名学生参加汉字听写大赛,为了解学生整体听写能力,从中抽取部分学生的成绩(得分取正整数,满分为100分)进行统计分析,请根据尚未完成的下列图表,解答问题:
组别 | 分数段 | 频数 | 频率 |
一 | 50.5~60.5 | 16 | 0.08 |
二 | 60.5~70.5 | 30 | 0.15 |
三 | 70.5~80.5 | 50 | 0.25 |
四 | 80.5~90.5 | m | 0.40 |
五 | 90.5~100.5 | n |
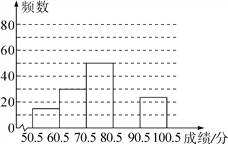
(1)本次抽样调查的样本是__________,样本容量为__________,表中m=__________,n=__________;
(2)补全频数分布直方图;
(3)若抽取的样本具有较好的代表性,且成绩超过80分为优秀,根据样本估计该校八年级学生中汉字听写能力优秀的约有多少人?