题目内容
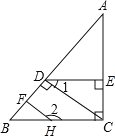
【题目】如图,已知AC⊥BC,CD⊥AB,DE⊥AC,∠1与∠2互补,判断HF与AB是否垂直,并说明理由(填空)

解:垂直.理由如下:
∵DE⊥AC,AC⊥BC,
∴∠AED=∠ACB=90°( 垂直的意义 ).
∴DE∥BC( ① )
∴∠1=∠DCB( ② )
∵∠1与∠2互补(已知).
∴∠DCB与∠2互补
∴ ③ (同旁内角互补,两直线平行)
∴∠BFH=∠CDB( ④ )
∵CD⊥AB,
∴∠CDB=90°.
∴∠BFH= ⑤ ( ⑥ ).
∴HF⊥AB.
【答案】垂直.理由见解析.
【解析】根据图形,由已知条件写出根据平行线的判定或性质,或根据性质或判定写出关系或度数即可.
∵DE⊥AC,AC⊥BC,
∴∠AED=∠ACB=90°(.
∴DE∥BC (同位角相等,两直线平行 )
∴∠1=∠DCB(两直线平行,内错角相等 )
∵∠1与∠2互补(已知).
∴∠DCB与∠2互补,
∴ FH∥CD
∴∠BFH=∠CDB( 两直线平行,同位角相等 )
∵CD⊥AB,
∴∠CDB=90°.
∴∠BFH= 90° ( 等量代换 ).
∴HF⊥AB.

练习册系列答案
相关题目