题目内容
已知某工厂计划用库存的302m3木料为某学校生产500套桌椅,供该校1250名学生使用,该厂生产的桌椅分为A,B两种型号,有关数据如下:
| 桌椅型号 | 一套桌椅所坐学生人数(单位:人) | 生产一套桌椅所需木材(单位:m3) | 一套桌椅的生产成本(单位:元) | 一套桌椅的运费(单位:元) |
| A | 2 | 0.5 | 100 | 2 |
| B | 3 | 0.7 | 120 | 4 |
设生产A型桌椅x(套),生产全部桌椅并运往该校的总费用(总费用=生产成本+运费)为y元.
(1)求y与x之间的关系式,并指出x的取值范围;
(2)当总费用y最小时,求相应的x值及此时y的值.
(1)y=﹣22x+62000,(240≤x≤250);
(2)生产甲型桌椅250套,乙型桌椅250套,最少总费用56500元.
解析试题分析:(1)利用总费用y=生产桌椅的费用+运费列出函数关系,根据需用的木料不大于302列出一个不等式,两种桌椅的椅子数不小于学生数1250列出一个不等式,两个不等式组成不等式组,得出x的取值范围;
(2)利用一次函数的增减性即可确定费用最少的方案以及费用.
试题解析:(1)设生产甲型桌椅x套,则生产乙型桌椅的套数(500﹣x)套,
根据题意得, ,
,
解这个不等式组得,240≤x≤250;
总费用y=(100+2)x+(120+4)(500﹣x)=102x+62000﹣124x=﹣22x+62000,
即y=﹣22x+62000,(240≤x≤250);
(2)∵y=﹣22x+62000,﹣22<0,
∴y随x的增大而减小,
∴当x=250时,总费用y取得最小值,
此时,生产甲型桌椅250套,乙型桌椅250套,最少总费用y=﹣22×250+62000=56500元.
考点:1、一元一次不等式组的应用;2、一次函数的应用

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 和x轴,y轴分别交于点E,F,点A是线段EF上一动点(不与点E重合),过点A作x轴垂线,垂足是点B,以AB为边向右作矩形ABCD,AB:BC=3:4。
和x轴,y轴分别交于点E,F,点A是线段EF上一动点(不与点E重合),过点A作x轴垂线,垂足是点B,以AB为边向右作矩形ABCD,AB:BC=3:4。

 (x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.

 (x>0)的图象上,
(x>0)的图象上,
 x+b,求n的值.
x+b,求n的值. 与
与 轴交于点A(-4,0),与
轴交于点A(-4,0),与 轴交于点B.
轴交于点B.
 处,点B若在
处,点B若在 处;
处; 的函数关系式;
的函数关系式; 的内接矩形,其中点P,Q在线段
的内接矩形,其中点P,Q在线段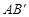 上,点M在线段
上,点M在线段 上,点N在线段AC上.若矩形PQMN的两条邻边的比为1∶2,试求矩形PQMN的周长.
上,点N在线段AC上.若矩形PQMN的两条邻边的比为1∶2,试求矩形PQMN的周长.