��Ŀ����
С���Ҿ���ѧУ8ǧ�ף������糿С���ﳵ��ѧ;�У����г�ͻȻ����̥����ǡ��·���б������㣬�����Ӻ����ˣ����ӿ��ٶ��ﳵ��У�����Ǹ���С������ξ�������һ��ͼ��ͼ�����С����ʻ·��s������ʱ��t֮��ĺ�����ϵ�������ͼ��ش��������⣺
��1��С���ﳵ��ʻ�˶���ǧ��ʱ�����г�����̥�������˼����ӣ�
��2��С�����öʱ�䵽ѧУ�ģ�
��3��С����ǰ���ٶȺ�������ٶȷֱ��Ƕ��٣�
��4��������г�δ����̥����С��һֱ����ǰ�ٶ���ʻ����ô����ʵ������絽���������ٷ��ӣ�
��1��3ǧ�ף�5���ӣ�
��2 С����30���ӵ�ѧУ��
��3��С����ǰ���ٶȣ�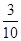 ǧ��/���ӣ�������ٶȣ�
ǧ��/���ӣ�������ٶȣ� ǧ��/���ӣ�
ǧ��/���ӣ�
��4���絽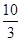 ���ӣ�
���ӣ�
���������������1��ͨ��ͼ���ϵĵ���������x��֮��Ĺ�ϵ��֪����ͼ��ͣ����5���ӣ�
��2��ͨ��ͼ���ϼ��ɿ���С����30���ӵ�ѧУ��
��3����Ӧ·�̳���ʱ�伴������ٶȣ�
��4���������ǰ�ٶ���Ҫ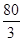 ���ӣ�����30��
���ӣ�����30��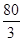 =
=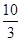 ������⣮
������⣮
�����������1��3ǧ�ף�5���ӣ�
��2��ͨ��ͼ���ϼ��ɿ���С����30���ӵ�ѧУ��
��3��С����ǰ���ٶȣ�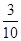 ǧ��/���ӣ�
ǧ��/���ӣ�
������ٶȣ� ǧ��/���ӣ�
ǧ��/���ӣ�
��4����ǰ�ٶ���Ҫ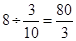 ���ӣ�30��
���ӣ�30��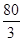 =
=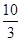 �����絽
�����絽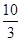 ���ӣ�
���ӣ�
���㣺һ�κ�����Ӧ�ã�

��֪ij�����ƻ��ÿ���302m3ľ��ΪijѧУ����500�����Σ�����У1250��ѧ��ʹ�ã��ó����������η�ΪA��B�����ͺţ��й��������£�
| �����ͺ� | һ����������ѧ����������λ���ˣ� | ����һ����������ľ�ģ���λ��m3�� | һ�����ε������ɱ�����λ��Ԫ�� | һ�����ε��˷ѣ���λ��Ԫ�� |
| A | 2 | 0.5 | 100 | 2 |
| B | 3 | 0.7 | 120 | 4 |
������A������x���ף�������ȫ�����β�������У���ܷ��ã��ܷ���=�����ɱ�+�˷ѣ�ΪyԪ��
��1����y��x֮��Ĺ�ϵʽ����ָ��x��ȡֵ��Χ��
��2�����ܷ���y��Сʱ������Ӧ��xֵ����ʱy��ֵ��
 ��ӳ��ij��Ʒ������������������֮��Ĺ�ϵ��
��ӳ��ij��Ʒ������������������֮��Ĺ�ϵ�� ��ӳ�˸ò�Ʒ�����۳ɱ���������֮��Ĺ�ϵ������������������۳ɱ�ʱ�ò�Ʒ�ſ�ʼӯ������ͼ��֪���ò�Ʒ���������ﵽ____________ �������ò�Ʒ����ӯ����
��ӳ�˸ò�Ʒ�����۳ɱ���������֮��Ĺ�ϵ������������������۳ɱ�ʱ�ò�Ʒ�ſ�ʼӯ������ͼ��֪���ò�Ʒ���������ﵽ____________ �������ò�Ʒ����ӯ����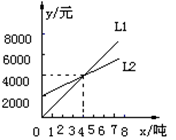
 ��˫����
��˫���� �ཻ��A��B���㣬��֪��A����2����1����
�ཻ��A��B���㣬��֪��A����2����1����
 ��
�� �ֱ��ʾij�մ�����8�㵽����11�㣬ÿ����ͨ��Ʊ�����۳��ij�Ʊ��
�ֱ��ʾij�մ�����8�㵽����11�㣬ÿ����ͨ��Ʊ�����۳��ij�Ʊ�� ���ţ���ÿ��������Ʊ�����۳��ij�Ʊ��
���ţ���ÿ��������Ʊ�����۳��ij�Ʊ�� ���ţ�������Ʊʱ��
���ţ�������Ʊʱ�� ��Сʱ���ĺ���ͼ��
��Сʱ���ĺ���ͼ��
 �������ͼ��ʾ����λ���ף�������Ŀ�δ�������Ϊ
�������ͼ��ʾ����λ���ף�������Ŀ�δ�������Ϊ �ף����۷���Ϊ�������ṩ�����������Żݷ�����
�ף����۷���Ϊ�������ṩ�����������Żݷ�����  �������
������� ��ʾ����һ�й���һ�û�����Ʒ�����ܽ���
��ʾ����һ�й���һ�û�����Ʒ�����ܽ��� ��ʾ�������й���һ�û�����Ʒ�����ܽ��ֱ����
��ʾ�������й���һ�û�����Ʒ�����ܽ��ֱ���� ��
�� ��
��
 ��x��0���ĺ���ͼ����D����P��һ�κ���
��x��0���ĺ���ͼ����D����P��һ�κ���
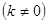 ��ͼ����÷���������ͼ���һ�������㣮
��ͼ����÷���������ͼ���һ�������㣮

 ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��