题目内容
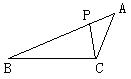
在等腰Rt△ABC中,∠C=90°,AC=BC,点D在AC边上,DE⊥AB,垂足为E,AD=2DC,则 的值为 .
的值为 .
 的值为 .
的值为 .
试题分析:解:∵AC=BC, ∠C=90°∴△ABC是等腰直角三角形,又∵DE⊥AB ∴△ADE也是等腰直角三角形,∴△ABC∽△ADE ,不妨令AC=3,∴AD=2,CD=1,则AE=DE=
 ∴S△ABC=
∴S△ABC=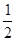 ×3×3=
×3×3= ,S△ADE=
,S△ADE=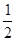 ×
× ×
× =1 S四边形DCBE=
=1 S四边形DCBE= -1=
-1=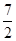 ∴S△ADE︰S四边形DCBE=
∴S△ADE︰S四边形DCBE= .四边形是不规则的四边形很难求出面积,可利用两个三角形的差求出。
.四边形是不规则的四边形很难求出面积,可利用两个三角形的差求出。点评:熟练掌握相似三角形的概念及判定条件,由题意知两三角形相似,从而得到边长,利用三角面积公式求出,四边形的面积用做差法求出,再进行比。本题难度不大属于基础题。

练习册系列答案
相关题目
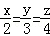 ,2x﹣3y+4z=22,求:代数式x+y﹣z的值.
,2x﹣3y+4z=22,求:代数式x+y﹣z的值.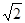 ,点A的坐标为(2,0),则E点的坐标为__________________。
,点A的坐标为(2,0),则E点的坐标为__________________。
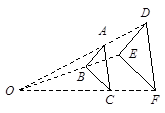
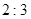 ,那么这两个相似三角形的面积比是 .
,那么这两个相似三角形的面积比是 .
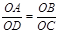 (2)CD ="2" AB(3)
(2)CD ="2" AB(3)