题目内容
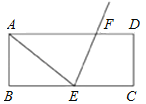
【题目】如图,长方形ABCD中,E为BC中点,作∠AEC的角平分线交AD于F点.若AB=6,AD=16,则FD的长度为何?( )
A.4 B.5 C.6 D.8
【答案】C
【解析】
试题分析:首先由矩形ABCD的性质,得BC=AD=16,已知E为BC中点,则BE=BC÷2=8,根据勾股定理在直角三角形ABE中可求出AE,再由∠AEC的角平分线交AD于F点,得∠AEF=∠CEF,已知矩形ABCD,AD∥BC,
则∠AFE=∠CEF,所以∠AEF=∠AFE,所以AF=AE,从而求出FD.
解:已知矩形ABCD,∴BC=AD=16,
又E为BC中点,
∴BE=![]() ×BC=
×BC=![]() ×16=8,
×16=8,
在直角三角形ABE中,
AE2=AB2+BE2=62+82=100,
∴AE=10,
已知矩形ABCD,
∴AD∥BC,
∴∠AFE=∠CEF,
又∠AEC的角平分线交AD于F点,
∴∠AEF=∠CEF,
∴∠AEF=∠AFE,
∴AF=AE=10,
∴FD=AD﹣AF=16﹣10=6,
故选:C.

练习册系列答案
相关题目