ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΦΉΓΔ““ΝΫΦ“¬ΧΜ·―χΜΛΙΪΥΨΗςΉ‘ΆΤ≥ωΝΥ–Θ‘Α¬ΧΜ·―χΜΛΖΰΈώΒΡ ’Ζ―ΖΫΑΗΘ°
ΦΉΙΪΥΨΖΫΑΗΘΚΟΩ‘¬ΒΡ―χΜΛΖ―”…ΝΫ≤ΩΖ÷Ήι≥…ΘΚΙΧΕ®Ζ―”Ο400‘ΣΚΆΖΰΈώΖ―”Ο5‘Σ/ΤΫΖΫΟΉΘΜ
““ΙΪΥΨΖΫΑΗΘΚ¬ΧΜ·ΟφΜΐ≤Μ≥§Ιΐ1000ΤΫΖΫΟΉ ±Θ§ΟΩ‘¬ ’»ΓΖ―”Ο5500‘ΣΘΜ¬ΧΜ·ΟφΜΐ≥§Ιΐ1000ΤΫΖΫΟΉ ±Θ§ΟΩ‘¬‘Ύ ’»Γ5500‘ΣΒΡΜυ¥Γ…œΘ§≥§Ιΐ≤ΩΖ÷ΟΩΤΫΖΫΟΉ ’»Γ4‘ΣΘ°
Θ®1Θ©«σΦΉΙΪΥΨ―χΜΛΖ―”ΟyΘ®‘ΣΘ©”κ¬ΧΜ·ΟφΜΐxΘ®ΤΫΖΫΟΉΘ©ΒΡΚ· ΐΫβΈω ΫΘ®≤Μ“Σ«σ–¥≥ωΉ‘±δΝΩΒΡΖΕΈßΘ©ΘΜ
Θ®2Θ©―Γ‘ώΡΡΦ“ΙΪΥΨΒΡΖΰΈώΘ§ΟΩ‘¬ΒΡ¬ΧΜ·―χΜΛΖ―”ΟΫœ…ΌΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©yΘΫ5x+400ΘΜΘ®2Θ©Β±0ΘΦxΘΦ1100 ±Θ§―Γ‘ώΦΉΙΪΥΨ―χΜΛΖ―”ΟΫœ…ΌΘ§Β±xΘΫ1100 ±Θ§ΝΫΦ“ΙΪΥΨ―χΜΛΖ―”Ο“Μ―υΘ§Β±xΘΨ1100 ±Θ§―Γ‘ώ““ΙΪΥΨ―χΜΛΖ―”ΟΫœ…ΌΘ°
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΦΉΙΪΥΨΖΫΑΗΘ§ΟΩ‘¬ΒΡ―χΜΛΖ―”…ΝΫ≤ΩΖ÷Ήι≥…ΘΚΙΧΕ®Ζ―”Ο400‘ΣΚΆΖΰΈώΖ―”Ο5‘Σ/ΤΫΖΫΟΉΘ§Ω…“‘–¥≥ωΦΉΙΪΥΨ―χΜΛΖ―”ΟyΘ®‘ΣΘ©”κ¬ΧΜ·ΟφΜΐxΘ®ΤΫΖΫΟΉΘ©ΒΡΚ· ΐΫβΈω ΫΘΜ
Θ®2Θ©ΗυΨί““ΙΪΥΨΖΫΑΗΘ§Ω…“‘–¥≥ω““ΙΪΥΨ―χΜΛΖ―”ΟyΘ®‘ΣΘ©”κ¬ΧΜ·ΟφΜΐxΘ®ΤΫΖΫΟΉΘ©ΒΡΚ· ΐΫβΈω ΫΘ§»ΜΚσάϊ”ΟΖ÷άύΧ÷¬έΒΡΖΫΖ®Θ§Ω…“‘ΒΟΒΫ―Γ‘ώΡΡΦ“ΙΪΥΨΒΡΖΰΈώΘ§ΟΩ‘¬ΒΡ¬ΧΜ·―χΜΛΖ―”ΟΫœ…ΌΘ°
ΫβΘΚΘ®1Θ©”…Χβ“βΩ…ΒΟΘ§
yΘΫ400+5xΘ§
Φ¥ΦΉΙΪΥΨ―χΜΛΖ―”ΟyΘ®‘ΣΘ©”κ¬ΧΜ·ΟφΜΐxΘ®ΤΫΖΫΟΉΘ©ΒΡΚ· ΐΫβΈω Ϋ «yΘΫ5x+400ΘΜ
Θ®2Θ©”…Χβ“βΩ…ΒΟΘ§
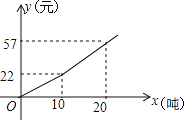
““ΙΪΥΨ―χΜΛΖ―”ΟyΘ®‘ΣΘ©”κ¬ΧΜ·ΟφΜΐxΘ®ΤΫΖΫΟΉΘ©ΒΡΚ· ΐΫβΈω Ϋ «yΘΫ![]() Θ§
Θ§
Β±0ΘΦxΓή1000 ±Θ§
Νν5x+400ΘΫ5500Θ§ΒΟxΘΫ1020Θ§
ΓΏ1020ΘΨ1000Θ§
ΓύΒ±0ΘΦxΓή1000Θ§―Γ‘ώΦΉΙΪΥΨΘΜ
Β±xΘΨ1000 ±Θ§
Νν5x+400ΘΦ5500+4Θ®x©¹1000Θ©Θ§ΒΟxΘΦ1100Θ§
Φ¥Β±1000ΘΦxΘΦ1100 ±Θ§―Γ‘ώΦΉΙΪΥΨ―χΜΛΖ―”ΟΫœ…ΌΘΜ
Νν5x+400ΘΫ5500+4Θ®x©¹1000Θ©Θ§ΒΟxΘΫ1100Θ§
Φ¥Β±xΘΫ1100 ±Θ§ΝΫΦ“ΙΪΥΨ―χΜΛΖ―”Ο“Μ―υΘΜ
Νν5x+400ΘΨ5500+4Θ®x©¹1000Θ©Θ§Β±xΘΨ1100Θ§
Φ¥Β±xΘΨ1100 ±Θ§―Γ‘ώ““ΙΪΥΨ―χΜΛΖ―”ΟΫœ…ΌΘ°
Ήέ…œΥυ ωΘΚΒ±0ΘΦxΘΦ1100 ±Θ§―Γ‘ώΦΉΙΪΥΨ―χΜΛΖ―”ΟΫœ…ΌΘ§
Β±xΘΫ1100 ±Θ§ΝΫΦ“ΙΪΥΨ―χΜΛΖ―”Ο“Μ―υΘ§
Β±xΘΨ1100 ±Θ§―Γ‘ώ““ΙΪΥΨ―χΜΛΖ―”ΟΫœ…ΌΘ°

 Οϊ ΠΒψ≤ΠΨμœΒΝ–¥πΑΗ
Οϊ ΠΒψ≤ΠΨμœΒΝ–¥πΑΗ ”Δ≤≈ΦΤΜ°ΤΎΡ©Βς―–œΒΝ–¥πΑΗ
”Δ≤≈ΦΤΜ°ΤΎΡ©Βς―–œΒΝ–¥πΑΗ