题目内容
【题目】问题提出：
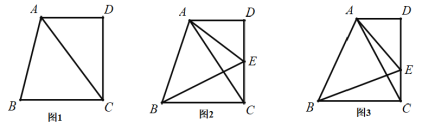
（1）如图1，在四边形
中，已知：
，
，
，
的面积为8，求
边上的高．
问题探究
（2）如图2在（1）的条件下，点
是
边上一点，且
，
，连接
，求
的面积
问题解决
（3）如图3，在（1）的条件下，点是边上任意一点，连接
、，若，的面积是否存在最小值；若存在，求出最小值；若不存在；请说明理由．
【答案】（1）4；（2）
；（3）存在，最小值为
【解析】
（1）作BC边上的高AM，利用三角形面积公式即可求解；
（2）延长DA，过B点作BF⊥DA于点F，作BH⊥AE于点H，易得四边形BCDF为矩形，在（1）的条件下BC=CD=4，则BCDF为正方形，由
，结合∠FAB=∠CBA可得∠FAB=∠EAB，从而推出BF=BH=4，易证Rt△BCE≌Rt△BHE，所以EH=CE=2，设AD＝a，则AF=AH=4-a，在Rt△ADE中利用勾股定理建立方程可求出a，最后根据S△ABE=
即可求解；
（3）辅助线同（2），设AD=a，CE=m，则DE=4-m，同（2）可得出m与a的关系式，设△ABE的面积为y，由y=得到m与y的关系式，再求y的最小值即可．
（1）如图所示，作BC边上的高AM，
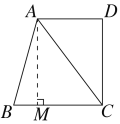
∵S△ABC=
∴
即BC边上的高为4；
（2）如图所示，延长DA，过B点作BF⊥DA于点F，作BH⊥AE于点H，
∵
，
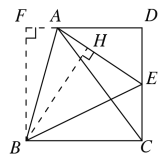
∴∠BCD=∠D=90°=∠F
∴四边形BCDF为矩形，
又∵BC=CD=4
∴四边形BCDF为正方形，
∴DF=BF=BC=4，
又∵AD∥BC
∴∠FAB=∠CBA
又∵∠EAB=∠CBA
∴∠FAB=∠EAB
∵BF⊥AF，BH⊥AE
∴BH=BF=4，
在Rt△BCE和Rt△BHE中，
∵BE=BE，BH=BC=4
∴Rt△BCE≌Rt△BHE（HL）
∴EH=CE=2
同理可证Rt△BAF≌Rt△BAH（HL）
∴AF=AH
设AD=a，则AF=AH=4-a
在Rt△ADE中，AD=a，DE=2，AE=AH+EH=4-a+2=6-a
由勾股定理得AD2+DE2=AE2，即
解得
∴AE=6-a=
S△ABE=
（3）存在，
如图所示，延长DA，过B点作BF⊥DA于点F，作BH⊥AE于点H，
同（2）可得CE=EH，AF=AH，
设AD=a，CE=EH=m，则DE=4-m，AF=AH=4-a
在Rt△ADE中，AD2+DE2=AE2，即
整理得
∴AE=AH+HE=
设△ABE的面积为y，
则y=
∴
整理得：
∵方程必有实数根
∴
整理得
∴
（注：利用求根公式进行因式分解）
又∵面积y≥0
∴
即△ABE的面积最小值为．
