题目内容
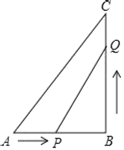
【题目】已知：如图，在△ABC中，∠B=90°，AB=5cm，BC=7cm．点P从点A开始沿AB边向点B以1cm/s的速度移动，点Q从点B开始沿BC边向点C以2cm/s的速度移动．如果P，Q分别从A，B同时出发．
(1)几秒后，△PBQ的面积等于6cm2？
(2)几秒后，四边形APQC的面积最小？最小值是多少？
【答案】（1）经过2秒或3秒钟，
的面积等于
（2）2.5秒后，四边形APQC的面积最小，最小值是
.
【解析】
（1）用t表示
、
，根据面积公式列出关于t的方程并解出，再结合实际情况进行检验；
（2）根据四边形APQC的面积等于△ABC面积减去△PBQ的面积，建立二次函数模型，在
范围内求最小值即可.
解：（1）设经过t秒钟，的面积等于
，则
，
，
根据题意得：
，
整理得：
，
解得：
，
，
∵
，
∴，
∴，，
答：经过2秒或3秒钟，的面积等于6．
（2）设四边形APQC的面积为y，则
，
即
，
∵抛物线对称轴为直线
，开口向上，
∴当时，图象先降后升，
∴当时，y最小，
答：2.5秒后，四边形APQC的面积最小，最小值是.
练习册系列答案
相关题目
