题目内容
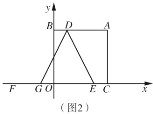
【题目】学校与图书馆在同一条笔直道路上，甲从学校去图书馆，乙从图书馆回学校，甲、乙两人都匀速步行且同时出发，乙先到达目的地．两人之间的距离
（米）与时间
（分钟）之间的函数关系如图所示．其中说法正确的是（ ）
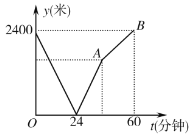
A.甲的速度是60米/分钟B.乙的速度是80米/分钟
C.点
的坐标为
D.线段
所表示的函数表达式为
【答案】D
【解析】
根据图象信息，甲60分钟行驶2400米，根据速度=路程÷时间可得甲的速度；由甲、乙两人的速度和为2400÷24=100米/分钟，减去甲的速度得出乙的速度，再根据“路程、时间与速度”的关系解答即可；求出乙从图书馆回学校的时间即A点的横坐标，用A点的横坐标乘以甲的速度得出A点的纵坐标，再将A、B两点的坐标代入，利用待定系数法即可求出线段AB所表示的函数表达式．
解：A、根据图象信息，甲的速度为2400÷60=40米/分钟，故A选项错误；
B、∵甲从学校去图书馆，乙从图书馆回学校，甲、乙两人都匀速步行且同时出发，t=24分钟时甲乙两人相遇，
∴甲、乙两人的速度和为2400÷24=100米/分钟，
∴乙的速度为100-40=60米/分钟，B选项错误；
C、乙从图书馆回学校的时间为2400÷60=40分钟，
40×40=1600，
∴A点的坐标为（40，1600），故C选项错误；
D、设线段AB所表示的函数表达式为y=kt+b，
∵A（40，1600），B（60，2400），
∴
，
解得：
，
∴线段
所表示的函数表达式为
，故D选项正确；
故选D.
【题目】蔬菜基地种植了娃娃菜和油菜两种蔬菜共
亩，设种植娃娃菜
亩，总收益为
万元，有关数据见下表：
成本（单位：万元/亩） | 销售额（单位：万元/亩） | |
娃娃菜 | 2.4 | 3 |
油菜 | 2 | 2.5 |
（1）求关于的函数关系式（收益 = 销售额 – 成本）；
（2）若计划投入的总成本不超过
万元，要使获得的总收益最大，基地应种植娃娃菜和油菜各多少亩？
（3）已知娃娃菜每亩地需要化肥
kg，油菜每亩地需要化肥
kg，根据（2）中的种植亩数，基地计划运送所需全部化肥，为了提高效率，实际每次运送化肥的总量是原计划的
倍，结果运送完全部化肥的次数比原计划少
次，求基地原计划每次运送多少化肥.
