题目内容
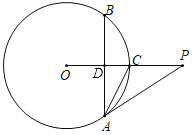
【题目】如图,![]() ,以
,以![]() 为圆心,2为半径作⊙
为圆心,2为半径作⊙![]() 交
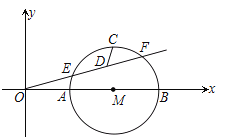
交![]() 轴于
轴于![]() 两点,射线
两点,射线![]() 交⊙
交⊙![]() 于
于![]() 两点,
两点,![]() 为弧
为弧![]() 的中点,
的中点,![]() 为
为![]() 的中点.当射线
的中点.当射线![]() 绕
绕![]() 点旋转时,
点旋转时,![]() 的最小值为( )
的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.不能确定
D.不能确定
【答案】C
【解析】
连接MD,如图,利用垂径定理得到MD⊥EF,则∠ODM=90![]() ,再根据勾股定理得到点D在以A点为圆心,2为半径的圆上,利用点与圆的位置关系可判断当D点为CA与⊙A的交点时,CD的值最小,此时CD=AC2=
,再根据勾股定理得到点D在以A点为圆心,2为半径的圆上,利用点与圆的位置关系可判断当D点为CA与⊙A的交点时,CD的值最小,此时CD=AC2=![]() .
.
∵![]() ,以
,以![]() 为圆心,2为半径作⊙
为圆心,2为半径作⊙![]() 交
交![]() 轴于
轴于![]() 两点,
两点,
连接AC,MC
∴OA=2,AM=2=CM=R
∵![]() 为弧
为弧![]() 的中点,AB为直径
的中点,AB为直径
∴∠AMC=90![]()
AC=![]()
连接MD,如图,
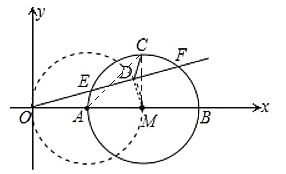
∵D为EF的中点,
∴MD⊥EF,
∴∠ODM=90![]() ,
,
∴点D在以A点为圆心,2为半径的圆上,
当D点为CA与⊙A的交点时,CD的值最小,此时CD=AC2=![]()
即CD的最小值为![]() .
.
故选C.

练习册系列答案
相关题目