题目内容
【题目】在平面直角坐标系![]() 中,
中,![]() ,
,![]() (
(![]() ),以
),以![]() 为直径画圆⊙
为直径画圆⊙![]() ,点
,点![]() 为⊙
为⊙![]() 上一动点.
上一动点.
(1)判断坐标原点![]() 是否在⊙
是否在⊙![]() 上,并说明理由;
上,并说明理由;
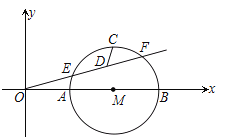
(2)若点![]() 在第一象限,过点
在第一象限,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,连接
,连接![]() ,且
,且![]() ,当
,当![]() 时,求线段
时,求线段![]() 的长:
的长:
(3)若点![]() 是
是![]() 的中点,试问随着
的中点,试问随着![]() 的变化点
的变化点![]() 的坐标是否发生变化,若不变,求出点
的坐标是否发生变化,若不变,求出点![]() 的坐标;若变化,请说明理由.
的坐标;若变化,请说明理由.

【答案】(1)原点![]() 是在
是在![]() 上,理由见解析;(2)
上,理由见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据圆周角定理即可得到结论;
(2)根据勾股定理得到AB=10,根据矩形的性质得到CD=PF=OE=4,PE=4,再求出![]() ,利用
,利用![]() 即可求解;
即可求解;
(3)过点C作CM⊥x轴于点M,CN⊥y轴于点N,由点C是![]() 的中点,得到
的中点,得到![]() ,推出AC=BC,根据全等三角形的性质得到BN=AM,CM=CN,推出四边形ONCM为正方形,于是得到结论.
,推出AC=BC,根据全等三角形的性质得到BN=AM,CM=CN,推出四边形ONCM为正方形,于是得到结论.
解(1)原点![]() 是在
是在![]() 上
上
理由:连接OP, ![]() 是
是![]() 的直径,
的直径,
![]()
![]()
![]()
∴原点![]() 是在
是在![]() 上;
上;
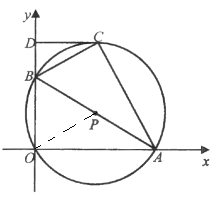
(2)连接PC,当![]() 时,
时, ![]()
![]() ,
,![]() ,r=5
,r=5
![]()
过![]() 作
作![]() 于
于![]()
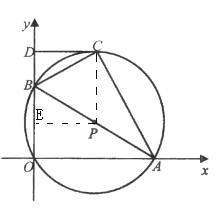
∵PE⊥BO
![]()
![]() 是
是![]() 的直径,
的直径,
![]()
![]()
![]()
![]()
![]()
![]()
![]() 轴,
轴,![]()
∴四边形![]() 是矩形,
是矩形,
![]()
![]()
![]() ,
,
(3)过点![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,
,
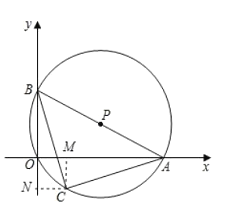
则四边形ONCM是矩形,
∴∠MCN=90![]() ,
,
∵∠ACB=90![]() ,
,
∴∠BCN=∠ACM,
∵点C是![]() 的中点,
的中点,
∴![]() ,
,
∴AC=BC,
在△BNC与△AMC中,
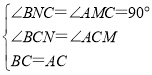 ,
,
∴△BNC≌△AMC,
所以![]() ,
,
∴四边形![]() 为正方形
为正方形
设![]() ,∴
,∴![]() ,
,
所以,![]()
得![]() ,
,
所以![]() .
.

 名校通行证有效作业系列答案
名校通行证有效作业系列答案【题目】计算能力是数学的基本能力,为了进一步了解学生的计算情况,初2020级数学老师们对某次考试中第19题计算题的得分情况进行了调查,现分别从A、B两班随机各抽取10名学生的成绩如下:
A班10名学生的成绩绘成了条形统计图,如下图,

B班10名学生的成绩(单位:分)分别为:9,8,9,10,9,7,9,8,10,8
经过老师对所抽取学生成绩的整理与分析,得到了如下表数据:
A班 | B班 | |
平均数 | 8.3 | a |
中位数 | b | 9 |
众数 | 8或10 | c |
极差 | 4 | 3 |
方差 | 1.81 | 0.81 |
根据以上信息,解答下列问题.
(1)补全条形统计图;
(2)直接写出表中a,b,c的值:a= ,b= ,c= ;
(3)根据以上数据,你认为A、B两个班哪个班计算题掌握得更好?请说明理由(写出其中两条即可): .
(4)若9分及9分以上为优秀,若A班共55人,则A班计算题优秀的大约有多少人?
【题目】某厂家销售一种产品,现准备从网上销售和市场直销两种销售方案中选择一种进行销售.由于受各种不确定因素影响,不同销售的方案会产生不同的成本和其它费用.设每月销售x件,网上销售月利润为w网(元),市场直销月利润为w市(元),具体信息如表:
每件售价(元) | 每件成本(元) | 月其他费用(元) | |
网上销售 | - | 20 | 45000 |
市场直销 | 120 | k |
|
其中k为常数,且30≤k≤50.月利润=月销售额-月成本-月其它费用.
(1)当x=500时,网上销售单价为______元.
(2)分别求出w网,w市与x间的函数解析式(不必写x的取值范围).
(3)若网上销售月利润的最大值与市场直销月利润的最大值相同,求k的值.
(4)如果某月要将3000件产品全部销售完,请你通过分析帮厂家做出决策,选择在网上销售还是市场直销才能使月利润较大?