题目内容
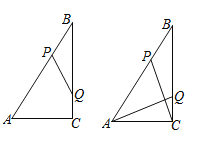
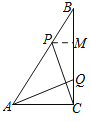
【题目】如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)当t为何值时,四边形ACQP的面积最小,最小值是多少?
(3)连接AQ,CP,若AQ⊥CP,求t的值.
【答案】(1)当t=1或t=![]() 时;(2)当t=1时,面积最小为18;(3)
时;(2)当t=1时,面积最小为18;(3)![]() .
.
【解析】【试题分析】(1)分类讨论: ![]() ,①当△BPQ
,①当△BPQ![]() △BAC时,
△BAC时,
则![]() =
=![]() ,又因为BP=5t,QC=4t,AC=6cm,BC=8cm,
,又因为BP=5t,QC=4t,AC=6cm,BC=8cm,
所以![]() =
=![]() ,解得:t=1;
,解得:t=1;
②当△BPQ![]() △BCA时,则
△BCA时,则![]() =
=![]() ,即
,即![]() =
=![]() ,解得:t=
,解得:t=![]() .
.
综合上述:当t=1或t=![]() 时,△BPQ与△ABC相似.
时,△BPQ与△ABC相似.
(2)做PD⊥BC于点D.根据四边形ACQP的面积等于总面积减去![]() 的面积,设四边形ACQP的面积为y,由题意得:
的面积,设四边形ACQP的面积为y,由题意得: ![]()
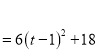
∵6>0,∴当t=1时,面积最小为18.
(3)过点P作PM⊥BC于点M,设AQ与CP相交于点N,则有PB=3t,MC=8-4t,
∵∠NAC+∠NCA=90°,∠PCM+∠NCA=90°,
∴∠NAC=∠PCM,
又∵∠ACQ=∠CMP=90°,
∴△ACQ∽CMP,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得:t=![]() .
.
【试题解析】
(1)①△BPQ与△ABC相似时,
则![]() =
=![]() ,
,
∵BP=5t,QC=4t,AC=6cm,BC=8cm,
∴![]() =
=![]() ,解得:t=1;
,解得:t=1;
②△BPQ与△BCA相似时,
则![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得:t=![]() .
.
综合上述:当t=1或t=![]() 时,△BPQ与△ABC相似.
时,△BPQ与△ABC相似.
(2)做PD⊥BC于点D.
设四边形ACQP的面积为y,由题意得:
![]()
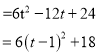
∵6>0,∴当t=1时,面积最小为18.
(3)过点P作PM⊥BC于点M,设AQ与CP相交于点N,则有PB=3t,MC=8-4t,
∵∠NAC+∠NCA=90°,∠PCM+∠NCA=90°,
∴∠NAC=∠PCM,
又∵∠ACQ=∠CMP=90°,
∴△ACQ∽CMP,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得:t=![]() .
.