题目内容
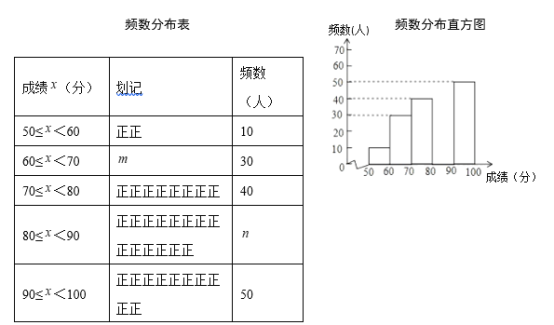
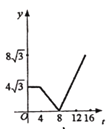
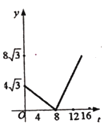
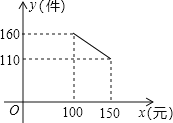
【题目】为发展“低碳经济”,某单位花12500引进了一条环保型生产线生产新产品,在生产过程中,每件产品还需成本40元,物价部门规定该产品售价不得低于100元/件且不得高于150元/件,每月销售量y(件)与销售单价x(元)之间的函数关系如图所示:
(1)求y与x之间的函数关系式,并写出x的取值范围;
(2)第一个月该单位是盈利还是亏损?求出当盈利最大或亏损最小时的产品售价;
(3)在(2)的前提下,即在第一个月盈利最大或亏损最小时,第二个月公司重新确定产品售价,能否使两个月共盈利达10800元?若能,求出第二个月的产品售价;若不能,请说明理由.
【答案】(1)y=﹣x+260(100≤x≤150);(2)第一个月公司亏损了,最小亏损为400元,此时商品售价定为150元/件;(3)每件商品售价定为120元时,公司两个月可盈利10800元
【解析】试题分析:(1)、首先设函数解析式为:y=kx+b,将图像上的两个点代入求出函数解析式;(2)、根据总利润=单件利润×数量-12500得出函数解析式,从而得出答案;(3)、根据题意得出方程,然后求出方程的解,根据x的取值范围得出x的值.
试题解析:(1)、设y=kx+b,由图象可得: ![]() ,解得:
,解得: ![]() ,
,
故函数解析式为:y=﹣x+260(100≤x≤150);
(2)、设公司第一个月的盈利为w元,
由题意得,w=y(x﹣40)﹣12500=﹣x2+300x﹣10400﹣12500,=﹣(x﹣150)2﹣400,
∴第一个月公司亏损了,最小亏损为400元,此时商品售价定为150元/件;
(3)、由题意,两个月共盈利10800元,得:﹣x2+300x﹣10400﹣400=10800,
解得x1=120,x2=180, 又∵100≤x≤150, ∴x=120,
∴每件商品售价定为120元时,公司两个月可盈利10800元.

 阅读快车系列答案
阅读快车系列答案【题目】某景区7月1日-7月7日一周天气预报如图,小丽打算选择这期间的一天或两天去该景区旅游,求下列事件的概率:
某景区一周天气预报
日期 | 天气 |
7月1日 | 晴 |
7月2日 | 晴 |
7月3日 | 雨 |
7月4日 | 阴 |
7月5日 | 晴 |
7月6日 | 晴 |
7月7日 | 阴 |
(1)随机选择一天,恰好天气预报是晴;
(2)随机选择连续的两天,恰好天气预报都是晴.