题目内容
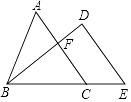
【题目】如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于 ![]() BC的长为半径作弧,两弧相交于点M、N;②作直线MN交AB于点D,连接CD,若CD=AD,∠B=20°,则下列结论中错误的是( )
BC的长为半径作弧,两弧相交于点M、N;②作直线MN交AB于点D,连接CD,若CD=AD,∠B=20°,则下列结论中错误的是( )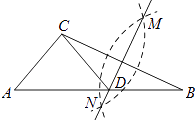
A.∠CAD=40°
B.∠ACD=70°
C.点D为△ABC的外心
D.∠ACB=90°
【答案】A
【解析】解:∵由题意可知直线MN是线段BC的垂直平分线,
∴BD=CD,∠B=∠BCD,
∵∠B=20°,
∴∠B=∠BCD=20°,
∴∠CDA=20°+20°=40°.
∵CD=AD,
∴∠ACD=∠CAD= ![]() =70°,
=70°,
∴A错误,B正确;
∵CD=AD,BD=CD,
∴CD=AD=BD,
∴点D为△ABC的外心,故C正确;
∵∠ACD=70°,∠BCD=20°,
∴∠ACB=70°+20°=90°,故D正确.
所以答案是:A.
【考点精析】本题主要考查了线段垂直平分线的性质和三角形的外接圆与外心的相关知识点,需要掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心才能正确解答此题.

练习册系列答案
相关题目