题目内容
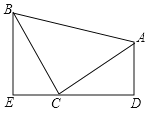
【题目】如图,已知AB是圆O的直径,弦CD⊥AB,垂足H在半径OB上,AH=5,CD=![]() ,点E在弧AD上,射线AE与CD的延长线交于点F.
,点E在弧AD上,射线AE与CD的延长线交于点F.
(1)求圆O的半径;
(2)如果AE=6,求EF的长.
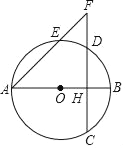
【答案】(1) 圆的半径为4.5;(2) EF=![]() .
.
【解析】
(1)连接OD,根据垂径定理得:DH=2![]() ,设圆O的半径为r,根据勾股定理列方程可得结论;
,设圆O的半径为r,根据勾股定理列方程可得结论;
(2)过O作OG⊥AE于G,证明△AGO∽△AHF,列比例式可得AF的长,从而得EF的长.
(1)连接OD,
∵直径AB⊥弦CD,CD=4![]() ,
,
∴DH=CH=![]() CD=2
CD=2![]() ,
,
在Rt△ODH中,AH=5,
设圆O的半径为r,
根据勾股定理得:OD2=(AH﹣OA)2+DH2,即r2=(5﹣r)2+20,
解得:r=4.5,
则圆的半径为4.5;
(2)过O作OG⊥AE于G,
∴AG=![]() AE=
AE=![]() ×6=3,
×6=3,
∵∠A=∠A,∠AGO=∠AHF,
∴△AGO∽△AHF,
∴![]() ,
,
∴![]() ,
,
∴AF=![]() ,
,
∴EF=AF﹣AE=![]() ﹣6=
﹣6=![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】下表中给出了变量x,与y=ax2,y=ax2+bx+c之间的部分对应值,(表格中的符号“…”表示该项数据已丢失)
x | ﹣1 | 0 | 1 |
ax2 | … | … | 1 |
ax2+bx+c | 7 | 2 | … |
(1)求抛物线y=ax2+bx+c的表达式
(2)抛物线y=ax2+bx+c的顶点为D,与y轴的交点为A,点M是抛物线对称轴上一点,直线AM交对称轴右侧的抛物线于点B,当△ADM与△BDM的面积比为2:3时,求B点坐标;
(3)在(2)的条件下,设线段BD与x轴交于点C,试写出∠BAD和∠DCO的数量关系,并说明理由.