题目内容
【题目】如图,已知△ABC和△CDE都是等边三角形,且A、C、E三点共线.AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下五个结论:① AD=BE;② ∠AOB=60°;③AP=BQ; ④△PCQ是等边三角形;⑤PQ∥AE.其中正确结论的有( )个

A.5B.4C.3D.2
【答案】A
【解析】
根据等边三角形的性质可得AC=BC,CD=CE,∠ACB=∠DCE,再求出∠ACD=∠BCE,然后利用“边角边”证明△ACD和△BCE全等,根据全等三角形对应边相等可得AD=BE,判断出①正确,全等三角形对应角相等可得∠ADC=∠BEC,∠CAD=∠CBE,再求出∠ACP=∠BCQ=60°,然后利用“边角边”证明△ACP和△BCQ全等,根据全等三角形对应边相等可得AP=BQ,CP=CQ,判断出③正确,根据∠AOB=∠PAC+∠BEC=∠QBC+∠BEC=∠BCA=60°,判断出②正确;判断出△PCQ为等边三角形,判断出④正确,根据等边三角形的性质可得∠CPQ=60°,得到∠ACB=∠CPQ,再根据内错角相等,两直线平行可得PQ∥AE,判断出⑤正确.
∵△ABC和△CDE均是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE,
∴∠ACB+∠ACE=∠DCE+∠ACE,
即∠ACD=∠BCE,
在△ACD和△BCE中,
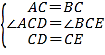 ,
,
∴△ACD≌△BCE(SAS),
∴AD=BE,(故①正确);
∴∠ADC=∠BEC,∠CAD=∠CBE,
∵∠BCQ=180°2×60°=60°,
∴∠ACP=∠BCQ=60°,
在△ACP和△BCQ中,
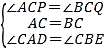 ,
,
∴△ACP≌△BCQ(ASA),
∴AN=BM,CM=CN,(故③正确);
∵∠AOB=∠PAC+∠BEC=∠QBC+∠BEC=∠BCA=60°,
故②正确;
∵∠BCQ=60°,CQ=CP,
∴△PCQ是等边三角形,(故④正确);
∴∠CPQ=60°,
∴∠ACB=∠CPQ=60°,
∴PQ∥BD,(故⑤正确);
综上所述,结论正确的是5个.
故选:A.











