题目内容
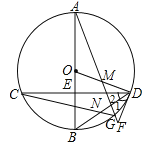
【题目】如图,在△ABC中,AB =AC,AD⊥BC于点D,AM是△ABC的外角∠CAE的平分线.
(1)求证:AM∥BC;
(2)若DN平分∠ADC交AM于点N,判断△ADN的形状并说明理由.

【答案】(1)证明见解析;(2)△ADN是等腰直角三角形,理由见解析
【解析】试题分析:(1)已知AB=AC,AD⊥BC,根据等腰三角形三线合一的性质可得∠BAD=∠CAD= ![]() ,再由AM平分∠EAC,根据角平分线的定义可得∠EAM=∠MAC=
,再由AM平分∠EAC,根据角平分线的定义可得∠EAM=∠MAC= ![]() ,根据平角的定义可得∠MAD=90°,根据同旁内角互补,两直线平行即可判定AM∥BC;(2)△ADN是等腰直角三角形,由(1)可得△ADN是直角三角形,因AM∥AD,根据平行线的性质可得∠AND=∠NDC,再由DN平分∠ADC,根据角平分线的定义和等量代换可得∠ADN=∠NDC=∠AND,根据等腰三角形的判定定理可得AD=AN,结论得证.
,根据平角的定义可得∠MAD=90°,根据同旁内角互补,两直线平行即可判定AM∥BC;(2)△ADN是等腰直角三角形,由(1)可得△ADN是直角三角形,因AM∥AD,根据平行线的性质可得∠AND=∠NDC,再由DN平分∠ADC,根据角平分线的定义和等量代换可得∠ADN=∠NDC=∠AND,根据等腰三角形的判定定理可得AD=AN,结论得证.
试题解析:
(1)∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD= ![]() .
.
∵AM平分∠EAC,
∴∠EAM=∠MAC= ![]() .
.
∴∠MAD=∠MAC+∠DAC= ![]() =
=![]() .
.
∵AD⊥BC,
∴![]() ,
,
∴∠MAD+![]() ,
,
∴AM∥BC.
(2)△ADN是等腰直角三角形,
理由是:∵AM∥AD,
∴∠AND=∠NDC,
∵DN平分∠ADC,
∴∠ADN=∠NDC=∠AND.
∴AD=AN.
∴△ADN是等腰直角三角形.

练习册系列答案
相关题目