题目内容
【题目】如图,△ ABC中,∠ ABC=90°,AB=BC,D在边 AC上,AE┴ BD于 E.

(1) 如图 1,作 CF⊥ BD于 F,求证:CF-AE=EF;
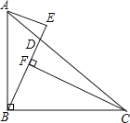
(2) 如图 2,若 BC=CD,求证:BD=2AE ;
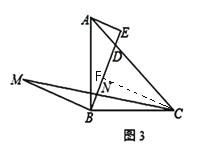
(3) 如图3,作 BM ⊥BE,且 BM=BE,AE=2,EN=4,连接 CM交 BE于 N,请直接写出△BCM的面积为______.
【答案】(1)见解析;(2)见解析;(3)5.
【解析】
(1)根据已知条件证明△ABE≌△BCF,即可求解;
(2)过点C作 CF⊥BD于点F,由(1)可知AE=BF=DF,故可求解;
(3)过点C作 CF⊥BD于点F,由(1)得△ABE≌△BCF,再证△BMN≌△FCN,根据S△BCM= S△BCN+S△MBN = S△BCN+S△CFN= S△BCM=![]() 即可求解.
即可求解.
(1) 证明:∵CF⊥BD于点F,AE⊥BD,
∴∠AEB=∠CFB=90°,
∴∠ABE+∠BAE=90°,
又∵∠ABC=90°,
∴∠ABE+∠CBF=90°,
∴∠BAE=∠CBF,
在![]() 中,
中,
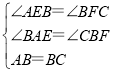
∴△ABE≌△BCF(AAS),
∴BE=CF,AE=BF,
∴CF-AE= BE-BF=EF.
(2)过点C作 CF⊥BD于点F,
∵BC=CD
∴BF=DF
由(1)得AE=BF,
∴AE=DF
∴BD=2AE
(3) 由(1)得△ABE≌△BCF
∵BM=BE
∴BM=CF
∵BM ⊥BE,∴∠MBN=∠CFN
又∠MNB=∠CNF
∴△BMN≌△FCN,∴BN=FN
∵AE=2,EN=4,
∴BF=AE=2,BN=![]() BF=1
BF=1
故BE=5,
∴S△BCM= S△BCN+S△MBN = S△BCN+S△CFN=![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目





