Question

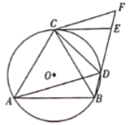
【题目】如图，四边形内接于⊙，，，垂足为．

(1)若，则 °．

(2)求证: ；

(3)若，，求的值．

Answer 1

【答案】（1）110；（2）见解析；（3）

【解析】

（1）由等腰三角形的性质求出∠ABC和∠ACB的度数，然后根据圆内接四边形的性质即可求出∠ADC的值；

（2）设，由等腰三角形的性质求表示出∠ABC和∠ACB，进而得出∠CBD，由圆周角定理得出∠DAC=∠CBD=，即可得出结论；

（3）由△ECD∽△EBA，可得BE=2CE，设CE=x，则BE=2x，AE=10-x，

在Rt△ABE中，求出x的值，再在Rt△BCE中即可求出BC的值．

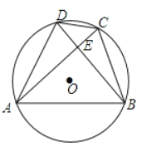
解：（1）∵AB=AC，，

∴∠ABC=∠ACB=70°，

∵四边形内接于⊙，

∴∠ADC=180°-70°=110°；

（2）设，

∵AB=AC，

∴∠ABC=∠ACB=，

∵BD⊥AC，

∴∠AEB=∠BEC=90°，

∴∠CBD=90°-=，

∵∠DAC=∠CBD，

∴；，

（3）∵∠ACD=∠ABD，∠BDC=∠BAC，

∴△ECD∽△EBA，

∴.

∵，，

∴，

∴BE=2CE，

设CE=x，则BE=2x，AE=10-x，

在Rt△ABE中，

(10-x)2+(2x)2=102，

解得

x1=4，x2=0（舍去），

∴CE=4，BE=8，

∴BC==．