题目内容
【题目】如图,四边形![]() 是
是![]() 的内接四边形,
的内接四边形,![]() ,
,![]() ,连接对角线
,连接对角线![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 的延长线上,且
的延长线上,且![]() ,
,![]() 的切线
的切线![]() 交
交![]() 于点
于点![]() .
.
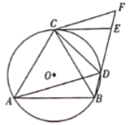
(1)求证:![]() ;
;
(2)求证:![]() .
.
【答案】(1)证明见解析;(1)证明见解析.
【解析】
(1)连接OC,由圆周角和AB=AC,易证明△ABC是正三角形,所以∠BCO=![]() ,又CE是切线,CE⊥OC,所以∠BCE=∠CBA,即可证明CE∥AB;
,又CE是切线,CE⊥OC,所以∠BCE=∠CBA,即可证明CE∥AB;
(2)因为∠BDC=![]() ,所以∠CDF=
,所以∠CDF=![]() ,又CF=DF,易证△CDF是正三角形,所以∠F=
,又CF=DF,易证△CDF是正三角形,所以∠F=![]() ,且BD+CD=BD+DF=BF,根据圆周角的性质易证∠ADC=∠ABC=∠F和∠CAB=∠CBF,又因为△ABC是正三角形,所以AC=BC,所以△ADC≌△BFC,即可得出证明AD=BD+CD.
,且BD+CD=BD+DF=BF,根据圆周角的性质易证∠ADC=∠ABC=∠F和∠CAB=∠CBF,又因为△ABC是正三角形,所以AC=BC,所以△ADC≌△BFC,即可得出证明AD=BD+CD.
证明:(1)如图,连接![]() ,
,
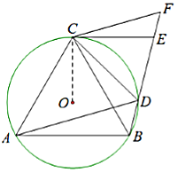
∵![]() 的内接四边形
的内接四边形![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() 是等边三角形,
是等边三角形,
∴![]() ,
,![]() ,
,
∵![]() 为
为![]() 的切线,
的切线,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() 、
、![]() 、
、![]() 、
、![]() 四点共圆,
四点共圆,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
∵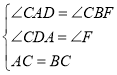 ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如下统计表.
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 11 | 15 | 23 | 28 | 18 | 5 |
(1)这天部分出行学生使用共享单车次数的中位数是 ,众数是 .
(2)这天部分出行学生平均每人使用共享单车约多少次?(结果保留整数)
(3)若该校某天有1500名学生出行,请你估计这天使用共享单车次数在3次以上(含3次)的学生有多少名.