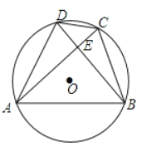
[题目]如图.楼房BD的前方竖立着旗杆AC．小亮在B处观察旗杆顶端C的仰角为45°.在D处观察旗杆顶端C的俯角为30°.楼高BD为20米．(1)求∠BCD的度数,(2)求旗杆AC的高度．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，楼房BD的前方竖立着旗杆AC．小亮在B处观察旗杆顶端C的仰角为45°，在D处观察旗杆顶端C的俯角为30°，楼高BD为20米．

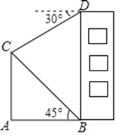
（1）求∠BCD的度数；

（2）求旗杆AC的高度．

【答案】（1）75°；（2）米

【解析】

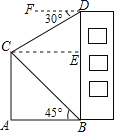
（1）过点C作CE⊥BD于E，则DF∥CE，AB∥CE，利用平行线的性质求得相关角的度数；

（2）在Rt△ECD、Rt△BCE中，利用正切三角函数解这两个直角三角形，求得CE的长度，进而即可求出答案．

（1）过点C作CE⊥BD于E，则DF∥CE，AB∥CE

∵DF∥CE

∴∠ECD＝∠CDF＝30°，

同理∠ECB＝∠ABC＝45°，

∴∠BCD＝∠ECD+∠ECB＝75°；

（2）在Rt△ECD中，∠ECD＝30°，

∵ ，

∴，

同理：BE＝CE，

∵BD＝BE+DE，

∴，解得：，

∴AC=BE=CE=，

答：旗杆AC的高度为米．

练习册系列答案

（1）图中a的值为　　；

（2）若要绘制该样本的扇形统计图，则成绩x在“70≤x＜80”所对应扇形的圆心角度数为　　度；

（3）此次比赛共有300名学生参加，若将“x≥80”的成绩记为“优秀”，则获得“优秀“的学生大约有　　人：

（4）在这些抽查的样本中，小明的成绩为92分，若从成绩在“50≤x＜60”和“90≤x＜100”的学生中任选2人，请用列表或画树状图的方法，求小明被选中的概率．

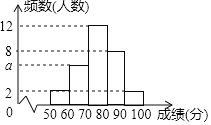
【题目】为进一步推动各级各类学校新型冠状病毒肺炎疫情防控工作，向广大教职工和学生普及新型冠状病毒肺炎疫情防控知识，做好师生返校前的卫生安全防护教育，上好开学第一课，省教育厅要求各级各类学校认真学习相关资料．某中学为了解学生的学习成果，对学生进行了新型冠状病毒肺炎防控知识测试，德育处随机从七、八两个年级各抽取20名学生的答卷成绩（单位：分）进行统计分析，过程如下：

收集数据

八年级：

85	80	95	100	90	95	85	65	75	85
90	90	70	90	100	80	80	90	95	75

七年级：

80	60	80	95	65	100	90	85	85	80
95	75	80	90	70	80	95	75	100	90

整理数据

成绩（分）
八年级	2	5
七年级	3	7	5	5

分析数据

统计量	平均数	中位数	众数
八年级	85．75	87．5
七年级	83．5		80

应用数据

（1）填空：__________，__________，__________，__________；

（2）看完统计数据，你认为对新型冠状病毒肺炎防护知识掌握更好的年级是__________；

（3）若八年级共有500人参与答卷，请估计八年级成绩大于90分的人数；

（4）在这次测试中，八年级学生甲与七年级学生乙的成绩都是85分，请判断两人在各自年级的排名谁更靠前，并说明理由．

【题目】现有5张除正面数字外完全相同的卡片，正面数字分别为1，2，3，4，5，将卡片背面朝上洗匀，从中随机抽出一张记下数字后放回，洗匀后再次随机抽出一张，则抽出的两张卡片上所写数字相同的概率______．

【题目】新型冠状病毒肺炎是一种急性感染性肺炎，其病原体是一种先前未在人体中发现的新型冠状病毒．市民出于防疫的需求，持续抢购防护用品．某药店口罩每袋售价20元，医用酒精每瓶售价15元．

（1）该药店第一周口罩的销售袋数比医用酒精的销售瓶数多100，且第一周这两种防护用品的总销售额为9000元，求该药店第一周销售口罩多少袋？

（2）由于疫情紧张，该药店为了帮助大家共渡难关，第二周口罩售价降低了，销量比第一周增加了，医用酒精的售价保持不变，销量比第一周增加了，结果口罩和医用酒精第二周的总销售额比第一周增加了，求的值．

【题目】位于湖北省荆州市滨江公园旁的万寿宝塔始建于明熹靖年间，周边风景秀丽．随着年代的增加，目前塔底低于地面约7米．某校学生先在地面处侧得塔顶的仰角为30°，再向古塔方向行进米后到达处，在处侧得塔顶的仰角为45°(如图所示)，已知古塔的整体高度约为40米，那么的值为_________米．(结果保留根式)