题目内容
【题目】已知,平面直角坐标系中,直线 y1=x+3与抛物线y2=﹣![]() +2x 的图象如图,点P是 y2 上的一个动点,则点P到直线 y1 的最短距离为()
+2x 的图象如图,点P是 y2 上的一个动点,则点P到直线 y1 的最短距离为()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
设过点P平行直线y1的解析式为y=x+b,当直线y=x+3与抛物线只有一个交点时,点P到直线y1的距离最小,如图设直线y1交x轴于A,交y轴于B,直线y=x+![]() 交x轴于C,作CD⊥AB于D,PE⊥AB于E,想办法求出CD的长即可解决问题.
交x轴于C,作CD⊥AB于D,PE⊥AB于E,想办法求出CD的长即可解决问题.
解:设过点P平行直线y1的解析式为y=x+b,
当直线y=x+3与抛物线只有一个交点时,点P到直线y1的距离最小,
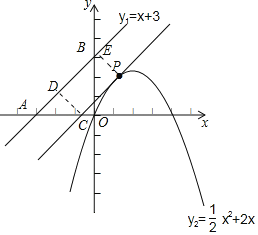
由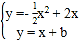 ,消去y得到:x2-2x+2b=0,
,消去y得到:x2-2x+2b=0,
当△=0时,4-8b=0,
∴b=![]() ,
,
∴直线的解析式为y=x+![]() ,
,
如图设直线y1交x轴于A,交y轴于B,直线y=x+![]() 交x轴于C,作CD⊥AB于D,PE⊥AB于E,则A(-3,0),B(0,3),C(-
交x轴于C,作CD⊥AB于D,PE⊥AB于E,则A(-3,0),B(0,3),C(-![]() ,0),
,0),
∴OA=OB=3,OC=![]() ,AC=
,AC=![]() ,
,
∴∠DAC=45°,
∴CD=![]() =
=![]() ,
,
∵AB∥PC,CD⊥AB,PE⊥AB,
∴PE=CD=![]() ,
,
故选:B.

 阅读快车系列答案
阅读快车系列答案【题目】洛阳某科技公司生产和销售A、B两类套装电子产品![]() 已知3套A类产品和2套B类产品的总售价是24万元;2套A类产品和3套B类产品的总售价是26万元
已知3套A类产品和2套B类产品的总售价是24万元;2套A类产品和3套B类产品的总售价是26万元![]() 公司生产一套A类产品的成品是
公司生产一套A类产品的成品是![]() 万元,生产B类产品的成本如下表:
万元,生产B类产品的成本如下表:
套数 | 1 | 2 | 3 | 4 |
|
总成本 | 8 | 12 | 16 | 20 |
|
![]() 该公司A类产品和B类产品的销售单价分别是多少万元?
该公司A类产品和B类产品的销售单价分别是多少万元?
![]() ①公司为了方便生产,只安排生产一类电子产品,且销售顺利,设生产销售该类电子产品x套:公司销售x套A类产品的利润
①公司为了方便生产,只安排生产一类电子产品,且销售顺利,设生产销售该类电子产品x套:公司销售x套A类产品的利润![]() ________;公司销售x套B类产品的利润
________;公司销售x套B类产品的利润![]() ________.
________.
②怎样安排生产,才能使公司获得的利润较高?
【题目】鄂北公司以10元/千克的价格收购一批产品进行销售,为了得到日销售量y(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如表:
销售价格x(元/千克) | 10 | 15 | 20 | 25 | 30 |
日销售量y(千克) | 300 | 225 | 150 | 75 | 0 |
(1)请你根据表中的数据确定y与x之间的函数表达式;
(2)鄂北公司应该如何确定这批产品的销售价格,才能使日销售利润W1元最大?
(3)若鄂北公司每销售1千克这种产品需支出a元(a>0)的相关费用,当20≤x≤25时,鄂北公司的日获利W2元的最大值为1215元,求a的值.