ĖâÄŋÄÚČÝ
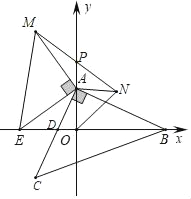
ĄūĖâÄŋĄŋČįÍžĢŽÔÚÆ―ÃæÖą―ĮŨøąęÏĩÖÐĢŽĄũABCΊĩČŅüÖą―ĮČý―ĮÐÎĢŽĄÏCABĢ―90ĄãĢŽĩãAĢŽĩãBĩÄŨøąę·ÖąðΊAĢĻ0ĢŽaĢĐĢŽBĢĻbĢŽ0ĢĐĢŽĮŌaĢŽbÂúŨãa2+b2Đ4aĐ8b+20Ģ―0ĢŽACÓëxÖá―ŧÓÚĩãDĢŪ
ĢĻ1ĢĐĮóĄũAOBĩÄÃæŧýĢŧ
ĢĻ2ĢĐĮóÖĪĢšĩãDΊACĩÄÖÐĩãĢŧ
ĢĻ3ĢĐĩãEΊxÖáĩÄļš°ëÖáÉÏĩÄķŊĩãĢŽ·ÖąðŌÔOAĢŽAEΊֹ―ĮąßÔÚĩÚŌŧĄĒķþÏóÏÞŨũĩČŅüÖą―ĮČý―ĮÐÎĄũOANšÍĩČŅüÖą―ĮČý―ĮÐÎĄũEAMĢŽÁŽ―ÓMN―ŧyÖáÓÚĩãPĢŽĘÔĖ―ūŋÏßķÎOEÓëAPĩÄĘýÁŋđØÏĩĢŽēĒÖĪÃũÄãĩÄ―áÂÛĢŪ
Ąūīð°ļĄŋĢĻ1ĢĐ4ĢŧĢĻ2ĢĐžû―âÎöĢŧĢĻ3ĢĐžû―âÎöĢŪ
Ąū―âÎöĄŋ
ĢĻ1ĢĐa2+b2Đ4aĐ8b+20Ģ―ĢĻaĐ2ĢĐ2+ĢĻbĐ4ĢĐ2Ģ―0ĢŽžīŋÉĮó―âĢŧ
ĢĻ2ĢĐÓÉĄÏABOĢ―ĄÏDAOĢŽÓÃ―âÖą―ĮČý―ĮÐÎĩÄ·―·ĻžīŋÉĮó―âĢŧ
ĢĻ3ĢĐÖĪÃũĄũAHMĄÕĄũEOAĢĻAASĢКͥũMPHĄÕĄũNPAĢĻAASĢĐĢŽžīŋÉĮó―âĢŪ
―âĢšĢĻ1ĢĐa2+b2Đ4aĐ8b+20Ģ―ĢĻaĐ2ĢĐ2+ĢĻbĐ4ĢĐ2Ģ―0ĢŽ
ÔōĢšaĢ―2ĢŽbĢ―4ĢŽ
SĄũAOBĢ―![]() OAOBĢ―4Ģŧ
OAOBĢ―4Ģŧ
ĢĻ2ĢĐĄÏOAB+ĄÏOBAĢ―90ĄãĢŽĄÏOAB+ĄÏDAOĢ―90ĄãĢŽ
ĄāĄÏABOĢ―ĄÏDAOĢŽ
OAĢ―2ĢŽOBĢ―4ĢŽÔōĢšABĢ―![]() ĢŽcosĄÏABOĢ―
ĢŽcosĄÏABOĢ―![]() Ģ―
Ģ―![]() ,
,
ADĢ―![]() Ģ―
Ģ―![]() Ģ―
Ģ―![]() ABĢ―
ABĢ―![]() ACĢŽ
ACĢŽ
žīĢšĩãDΊACĩÄÖÐĩãĢŧ
ĢĻ3ĢĐđýĩãMŨũMHĄÍyÖá―ŧÓÚĩãHĢŽ
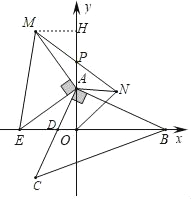
ĄßĄÏMAH+ĄÏEAOĢ―90ĄãĢŽĄÏMAH+ĄÏHMAĢ―90ĄãĢŽ
ĄāĄÏHMAĢ―ĄÏEAOĢŽ
ÓÖĄÏMHAĢ―ĄÏAOEĢ―90ĄãĢŽAEĢ―AMĢŽ
ĄāĄũAHMĄÕĄũEOAĢĻAASĢĐĢŽ
ĄāAHĢ―OEĢŽMHĢ―OAĢ―ANĢŽ
ÓÖĄÏMHAĢ―ĄÏNAPĢ―90ĄãĢŽĄÏMPHĢ―ĄÏAPNĢŽ
ĄāĄũMPHĄÕĄũNPAĢĻAASĢĐĢŽ
ĄāAPĢ―PHĢ―![]() AHĢ―
AHĢ―![]() OEĢŪ
OEĢŪ

 Õã―ÃûÐĢÃûĘĶ―ðūíÏĩÁÐīð°ļ
Õã―ÃûÐĢÃûĘĶ―ðūíÏĩÁÐīð°ļ ČŦÓÅģåīĖ100·ÖÏĩÁÐīð°ļ
ČŦÓÅģåīĖ100·ÖÏĩÁÐīð°ļ